The shear modulus is also known as the modulus of rigidity, and it is the measurement of the rigidity of the material or body given by the ratio of shear stress to shear strain. Often it is denoted by the G or sometimes by the μ or S as well.
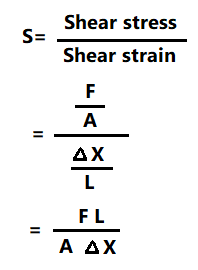
Units of Shear Modulus of Rigidity
Pa is the SI unit of the shear modulus, but generally, its values are expressed in the Gigapascals (GPa). In the English units, the shear modulus of rigidity is given in the terms of the pounds per square inch (PSI) or Kilo pounds per square inches (Ksi). The larger values of the shear modulus indicate the high rigidity of the solid. In other words, for the deformation of the solids with high values of shear modulus, more force is required. The smaller values of the shear modulus show that the solid is flexible or soft and a little force is required for causing deformation in it. The value of shear modulus for the fluids is zero, and any applied force can cause deformation in its surface.

The equation for Shear Modulus of Rigidity
The shear modulus of rigidity can be determined by measuring the deformation in the solid that happens due to the applied force parallel to the surface of the solid, while an opposite force is acting on the opposite surface that holds the solid in the place. The shear can be considered as pushing against one side of the block, with the friction as a source of the opposing force. Another example can be the attempt to cut the hair or wire with the help of scissors. The equation for the shear modulus is as below.
G = τxy / γxy = F/A / Δx/l = Fl / AΔx
Here G is used to denote the shear modulus of rigidity. τxy represents the shear stress, γxy is used for denoting the shear strain. A represents the area over which the force is acting. Δx shows the transverse displacement. Whereas, l represents the initial length.
Values of Shears Modulus of Rigidity
The values for the shear modulus of rigidity are determined at room temperature. The bigger values of the shear modulus show that the material is more rigid and bigger force is required for causing the changes in the material. Lower values of the shear modulus are associated with flexible and soft materials. While the basic and alkaline earth metals have intermediate values. However, higher values are associated with the alloys and transition metals.