We have studied that magnitude of the velocity of the $i^{th}$ particle in a rigid body rotating about a fixed axis is,
$v_{i}=r_{i}d\theta /dt=r_{i}\omega $
The kinetic energy of the $i^{th}$ particle of mass $m_{i}$ is given by,
![]()
The total kinetic energy of the rigid body is,
![]()
As angular velocity ω is same for all the particles in the body, therefore,
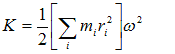
Or, $K=1/2 I \omega ^{2}$ ……………………………… (1)
Where
![]()
is known as rotational inertia or moment of inertia of the rotating body.
Moment of inertia of a rigid body is the mass of each particle multiplexed by its squared distance from the axis of rotation and then summing over these products for all the particles in the body.
The SI unit of moment of inertia is $Kgm^{2}.$
The equation (1) is analogous to the translational kinetic energy where moment of inertia is analogous to mass $m$ (or inertia) and angular velocity is analogous to velocity $v$.
Moment of inertia of the uniform rod about a perpendicular bisector:
Consider a uniform rod of mass $M$ and length $L$.
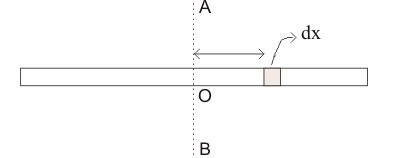
Figure: 20.a
To calculate the moment of inertia of the rod about the bisector AB, let the point $O$ be the origin of the rod. Also, consider an element of the rod between the distance $x$ and $x+dx$ from the origin $O$. Since the rod is uniform so its density $\rho =M/L$.
Hence, mass of the element $dm=dx(M/L)$
$x$ is the perpendicular distance from line AB, so the moment of inertia of the element about AB is given by,
![]()
For $x=-L/2$, the element is at the left end of the rod. As $x$ changes from $-L/2 to +L/2$, the element covers the whole rod.
Thus the moment of inertia of the entire rod about AB is given by,
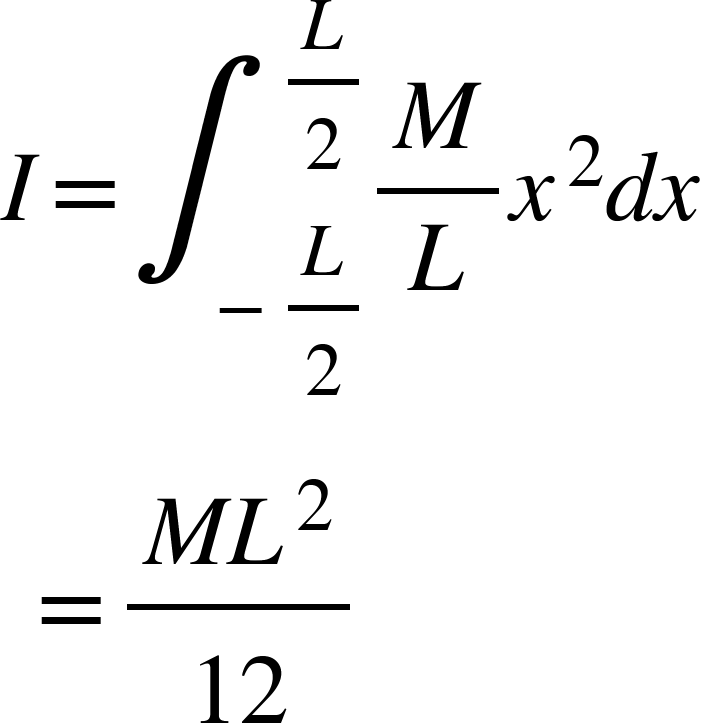
Moment of inertia of the uniform circular plate about its axis:
Consider a uniform circular plate of mass and radius as shown below.
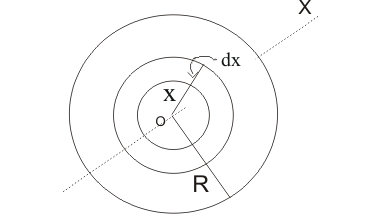
Figure: 20.b
Let O be the center of the plate and $OX$ is the axis perpendicular to the plane.
Let us draw two concentric circles of radii $x$ and $x+dx$ having these centers at $O$, so that they form a ring.
Area of the ring: $=2\pi xdx$
Mass of the ring would be
![]()
Moment of inertia of this ring about axis $OX$ is given by,
$dI=\frac{2Mxdx}{R^{2}}x^{2}$
Or,
$dI=\frac{2Mdx}{R^{2}}x^{3}$
Moment of inertia of the entire plate is given by,
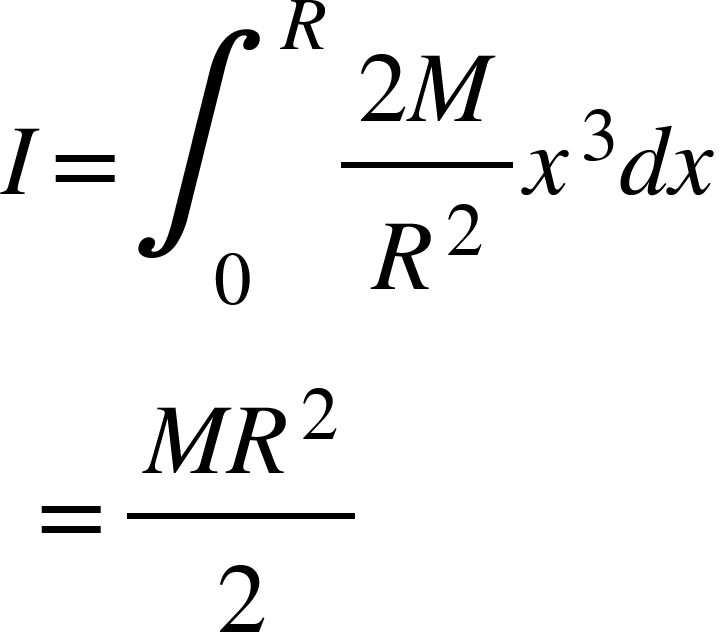 .
.