When an object moves in a circular path at a constant speed, then the motion of the object is called uniform circular motion. In a uniform circular motion, the object accelerates because of the constantly changing the direction of the velocity.
Centripetal acceleration:
Let us consider an object moving in a circular path of radius R and O is the centre. Suppose the velocity of the object at point P is 
and in time $\Delta t$, the velocity at point Q is 
.
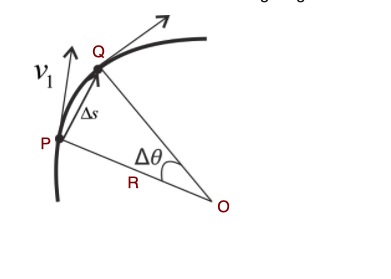
Figure:9.a
When the object moves from P to Q, there is a change of velocity vector, and we say it 
.
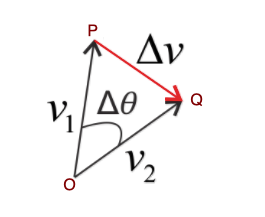
Figure:9.b
Since the velocity vectors 
and 
are always perpendicular to the position vectors, the angle between them is $\Delta \theta $.
Now from figure 9.a and 9.b, it can be seen that both the triangles are isosceles and the angle $\Delta \theta $ in both the triangles are the same.
Then, $\frac{\Delta v}{v_{1}}=\frac{\Delta s}{R}$
Or, $\Delta v=\frac{v_{1}}{R}\Delta s$
Since the average acceleration 
is along $\Delta v$, the average acceleration is perpendicular to $\Delta s$.
Therefore, the magnitude of 
is given by,
The limiting value of the acceleration is given by,
Or, 
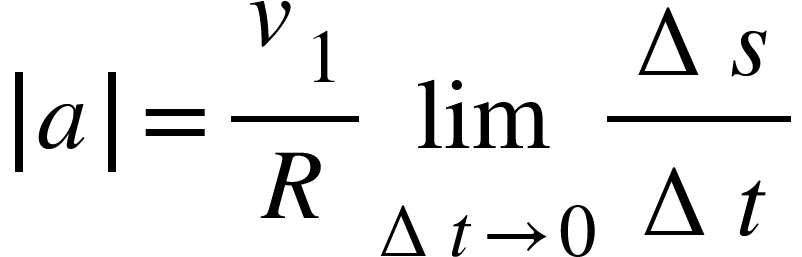
But the limiting value of $\Delta s/\Delta t$is the speed 
of the object at point P.
The point P can be any point in the circular path, therefore, we can consider that $v$ is the speed of the object at any point in the circular path.
So, the above equation becomes,
…………………… (1)
The magnitude of the instantaneous normal acceleration is equal to the square of the speed divided by the radius of the circular path. Its direction is perpendicular to speed and acts along the inward direction towards the center of the circle.
Hence, the equation (1) gives the formula of centripetal acceleration. The term centripetal means seeking the center.
Angular velocity:
The velocity $v$ at any point of the circular motion is tangential to the circle at that point. The distance along the circumference from P to Q is given by, $\Delta s=R\Delta \theta $ where $\theta $ is the angle between position vectors or velocity vectors.
The magnitude of velocity is,
……………………. (2)
Since the radius of the circular path remains constant, we can write,
…………………………… (3)
Where $\omega $ is the angular velocity defined as the rate of change of angle swept by radius with time.
From equations (2) and (3), we get
$v=\omega R$ ……………………….. (4)
Equation (4) gives the expression for angular speed $\omega $.
Centripetal acceleration in terms of angular speed $\omega $ is given by,
The time taken by the object to make one revolution is called the time period T and the number of revolution made in one second is called the frequency ($f$=1/T) of revolution.
Now, distance moved by the object is $2\pi R$ in time period T.
So, $v=2\pi R/T$
Or, $v=2\pi Rf$ ……………………… (5)
And $\omega =2\pi f$ …………………… (6)
Angular acceleration $\vert a\vert =4\pi ^{2}f^{2}R$ ………………… (7)
