Center of mass is the point where the whole mass of the system can be supposed to be concentrated and the motion of the system can be defined in terms of the center of mass.
Position of center of mass for the two-particle system:
Consider a system of two point masses $m_{1}$and $m_{2}$,whose position vectors at time $t$ with respect to the origin O are ${r_{1}}$ and ${r_{2}}$ respectively as shown below.
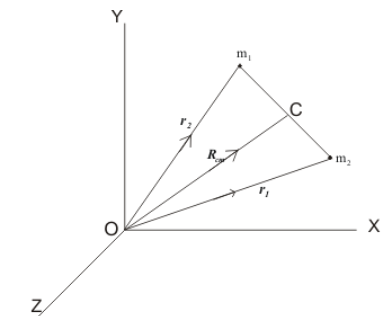
Figure:15.a
The total force ${F_{1}} $ that is acting on point mass $m_{1}$ consists of two parts.
Where ${F}_{1(ext)}$= external force acting on the system
${F}_{12}$= Force due to $m_{2}$.
Similarly for point mass $m_{2}$,
The equation of motion for point mass can be obtained using the second law of motion,
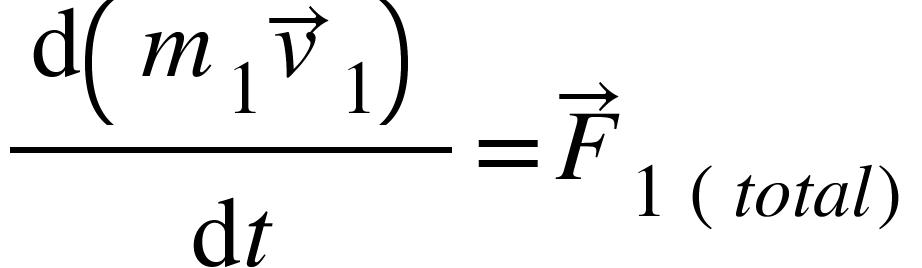…………….. (1)
And for point mass $m_{2}$,
……………….. (2)
Adding equations (1) and (2), we get,
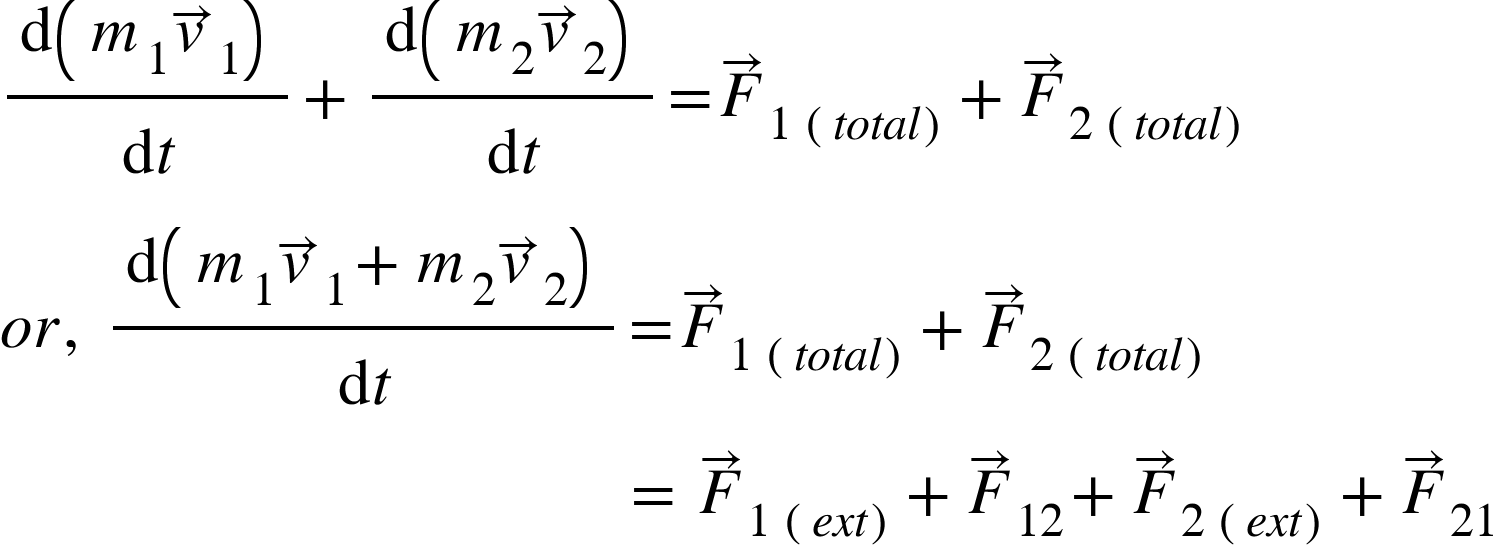……………….. (3)
Also, we have from Newton’s third law of motion,
Then from equation (3), we have,
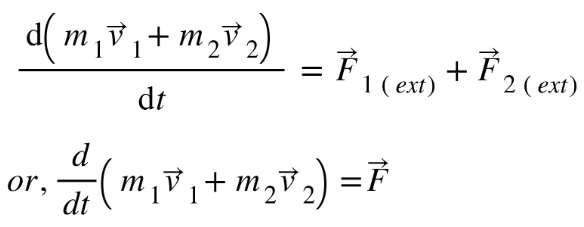…………………… (4)
Now,
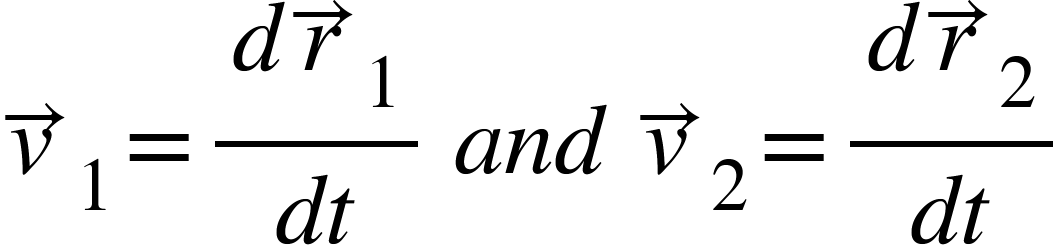
So, from equation (4), we get,
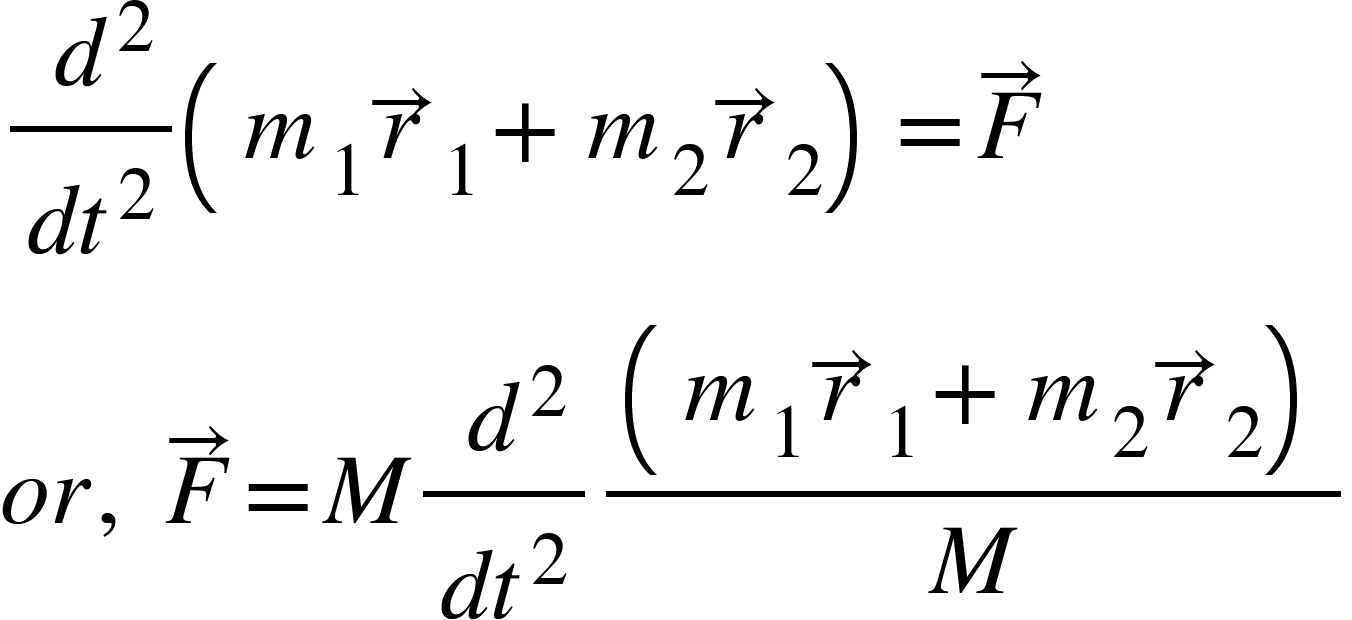
This equation is clearly the equation of motion of a hypothetical object of mass $M=m_{1}+m_{2}$.
The position of this point at any time is given by the position vector ${R}_{CM}$such that
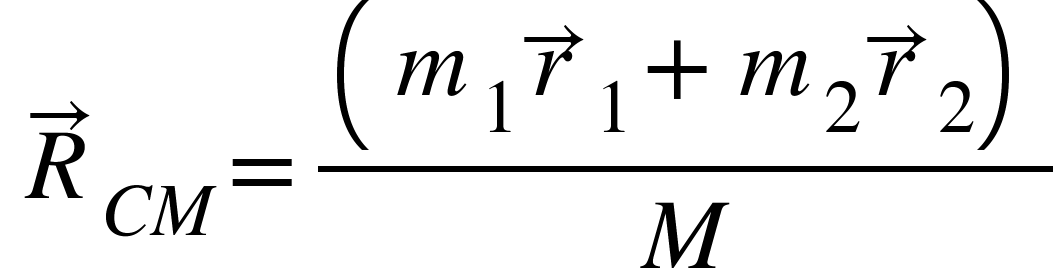
${R}_{CM}$is the center of mass of the two-particle system.
If $m_{1}=m_{2}$then,
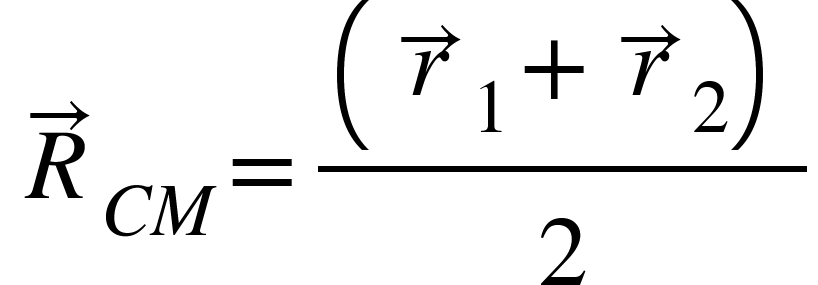
Thus, the center of mass of two equal masses lies exactly at the center of the line joining the two masses.
If $(x_{1, }y_{1})$ and $(x_{2, }y_{2})$ are the coordinates of the locations of two particles , then the coordinates of their center of mass is given by,
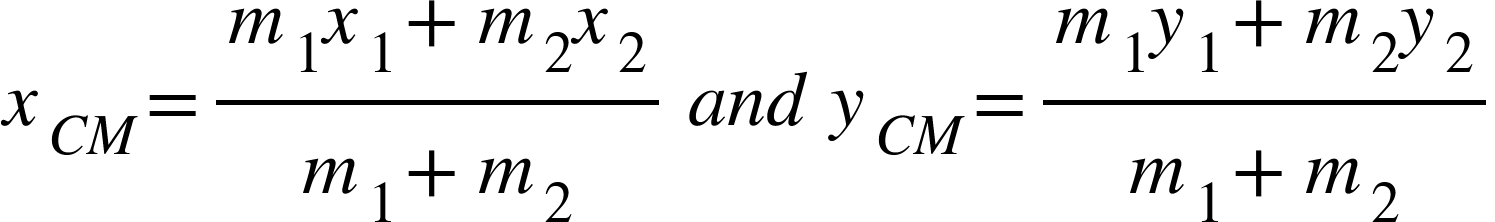
The center of mass for the many-particle system is given by,
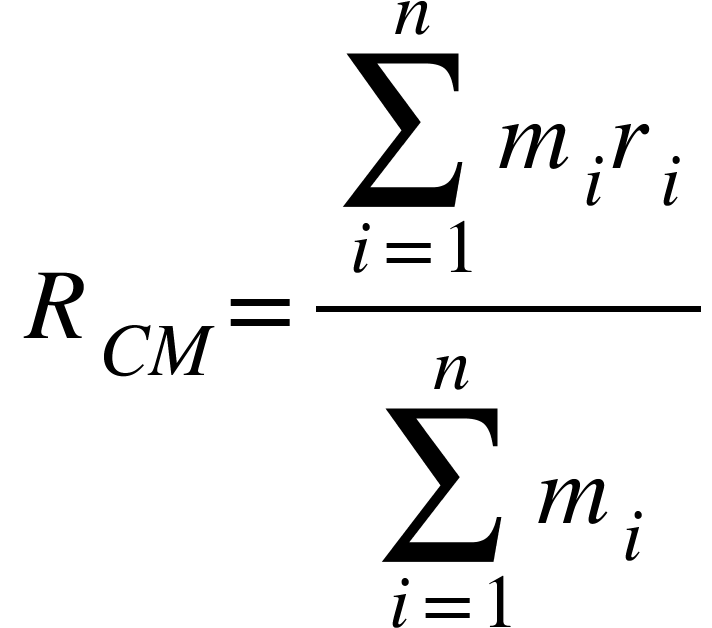
Points to remember:
- The position of the center of mass is independent of the coordinate system.
- The position of the center of mass depends upon the shape of the body and the distribution of mass across the body.
- Symmetrical bodies in which the distribution of mass is homogeneous, the center of mass coincides with the geometrical center.