System of Particles and Collision

A collision between two particles is defined as the mutual interaction between particles for a short interval of time as a result of which energy and momentum of the particle change.

In the collision of two particles, the law of conservation of momentum always holds true but in some collisions, kinetic energy is not always conserved.

Collisions are of two types on the basis of the conservation of energy.

Perfectly elastic collision:

In a perfectly elastic collision, both momentum and kinetic energy of a system are conserved. This type of collision mostly takes place between the atoms, electrons, and protons.

Characteristics of elastic collision:

1. total momentum is conserved.
2. total energy is conserved.
3. total kinetic energy is conserved.
4. total mechanical energy is not converted into any other form of energy.

Consider two particles of masses are $m_{1}$and $m_{2}$ collide with each other with velocities $u_{1}$and $u_{2}$. After collision, their velocities become $v_{1}$and $v_{2}$ respectively.

Considering the collision to be elastic, then from the law of conservation of momentum we have,

$m_{1}$$u_{1}+m_{2}u_{2}=m_{1}v_{1}+m_{2}v_{2}$ and from the law of conservation of energy we have,

Perfectly inelastic collision:

In perfectly inelastic collisions, the momentum of the system is conserved but kinetic energy is not conserved.

Characteristics of inelastic collision:

1. total momentum is conserved.
2. total energy is conserved.
3. total kinetic energy is not conserved.
4. mechanical energy may be converted into other forms of energy.

Consider two particles of masses are $m_{1}$and $m_{2}$ collide with each other with velocities $u_{1}$and $u_{2}$. Considering the collision to be inelastic, then these two particles would stick to each other and after collision they move with velocity $v$ . Then we have,

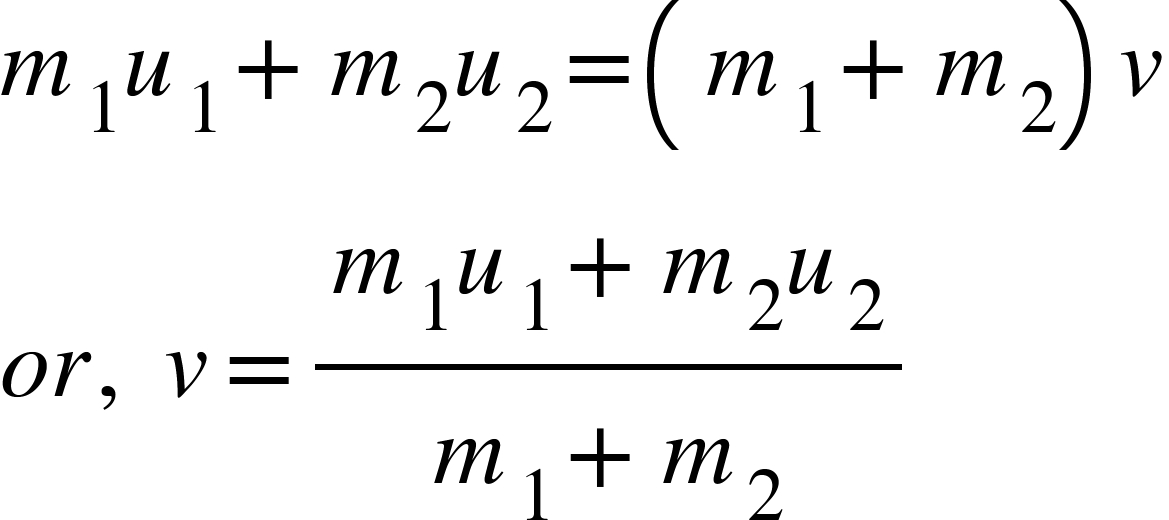
Kinetic energy of particles before collisions is,

and kinetic energy after collisions is ,

Using the law of conservation of energy, we get

Where $Q$ is the loss in kinetic energy of particles during the collision.

Head on elastic collision of two particles:

From the law of conservation of momentum we have,

$m_{1}$$u_{1}+m_{2}u_{2}=m_{1}v_{1}+m_{2}v_{2}$ …………. (1)

and from the law of conservation of energy we have,

    ……………. (2)

Rearranging equation (1) and (2), we get

$m_{1}(u_{1}-v_{1})=$ $m_{2}(v_{2}-u_{2})$ ………………….. (3)

And

……………. (4)

Dividing equation (4) by (3), we get $(u_{1}+v_{1})=$$(u_{2}+v_{2})$ Or, $u_{2}-u_{1}=-(v_{2}-v_{1})$ …………….. (5)

$u_{2}-u_{1}$ is the relative velocity of the second particle with respect to the first particle before the collision and is the relative velocity of the second particle with respect to the first particle after the collision.

Equation (5) can be written as, $v_{1}=v_{2}-u_{1}+u_{2}$ ……………… (6)

$v_{2}=v_{1}+u_{1}-u_{2}$ ……………… (6)

Now putting the value of $v_{1}$ in equation (3) we get, $m_{1}(u_{1}-v_{2}+u_{1}-u_{2})=$ $m_{2}(v_{2}-u_{2})$ Or, $-m_{1}v_{2 }-m_{2}v_{2}+2$ $m_{1}u_{1}-m_{1}u_{2}-m_{2}u_{2}=0$ On solving the equation we get the value $v_{2}$ of as

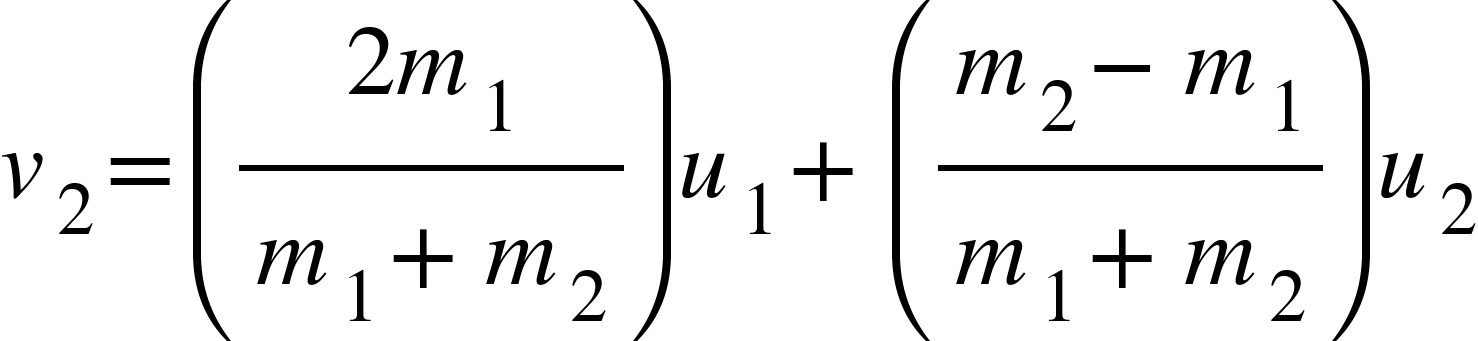    …………….. (7)

Similarly putting the value of $v_{2}$ in equation (3) we get,

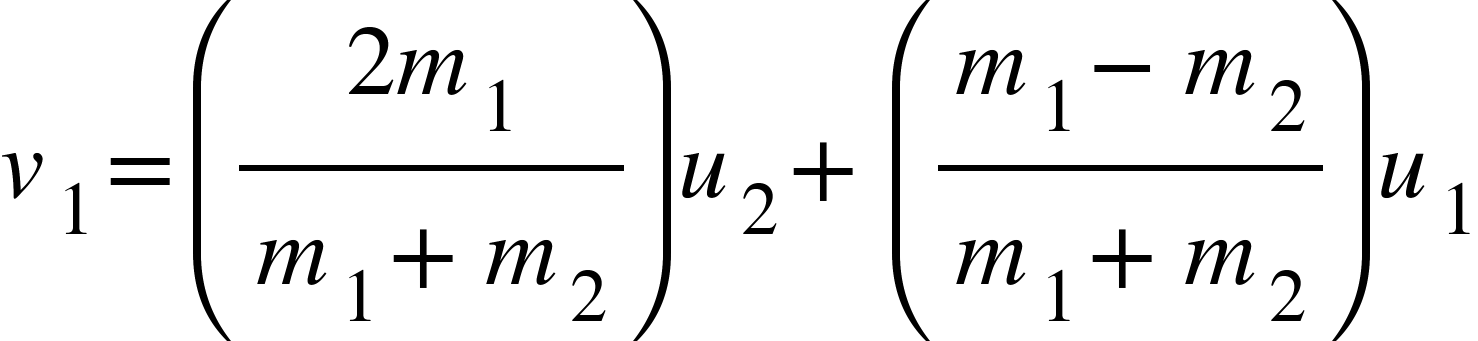 …………….. (8)

 

Points to remember:

When $m_{1}=m_{2}$then from equation (7) and (8) , $v_{2}=u_{1}$ and $v_{1}=u_{2}$.

Thus if two particles of equal masses suffer head-on elastic collision then the particles will exchange their velocities.