Velocity and Acceleration of Center of Mass

The center of mass for many particle system is given by,

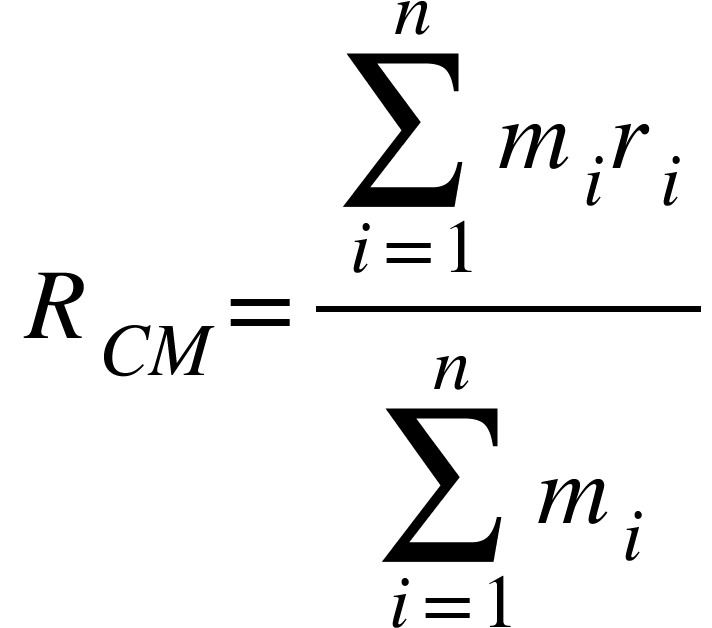
$<math xmlns="http://www.w3.org/1998/Math/MathML"><mspace linebreak="newline"/><mo> </mo><msub><mi>R</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>=</mo><mfrac><mrow><mstyle displaystyle="true"><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover></mstyle><msub><mi>m</mi><mi>i</mi></msub><msub><mi>r</mi><mi>i</mi></msub></mrow><mrow><mstyle displaystyle="true"><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover></mstyle><msub><mi>m</mi><mi>i</mi></msub></mrow></mfrac></math>$

Differentiating the above equation, we get,

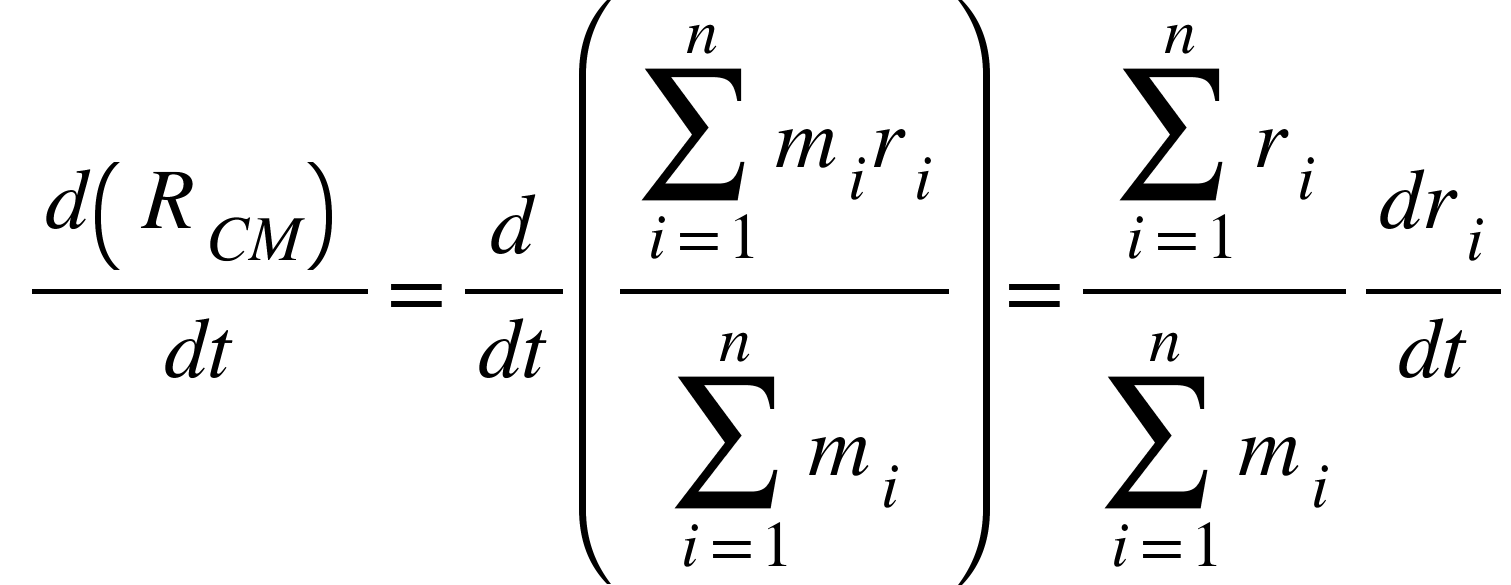
$<math xmlns="http://www.w3.org/1998/Math/MathML"><mspace linebreak="newline"/><mo> </mo><mfrac><mrow><mi>d</mi><mfenced><msub><mi>R</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub></mfenced></mrow><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><mo>=</mo><mfrac><mi>d</mi><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><mfenced><mfrac><mstyle displaystyle="true"><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msub><mi>r</mi><mi>i</mi></msub></mstyle><mstyle displaystyle="true"><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub></mstyle></mfrac></mfenced><mo>=</mo><mfrac><mrow><mstyle displaystyle="true"><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover></mstyle><msub><mi>r</mi><mi>i</mi></msub></mrow><mrow><mstyle displaystyle="true"><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover></mstyle><msub><mi>m</mi><mi>i</mi></msub></mrow></mfrac><mfrac><mrow><mi>d</mi><msub><mi>r</mi><mi>i</mi></msub></mrow><mrow><mi>d</mi><mi>t</mi></mrow></mfrac></math>$

But, $d(R_{CM})/dt=V_{CM}$= velocity of center of mass and

$d(r_{i})/dt=v_{i}$= velocity of i’th particle of the system

Therefore,

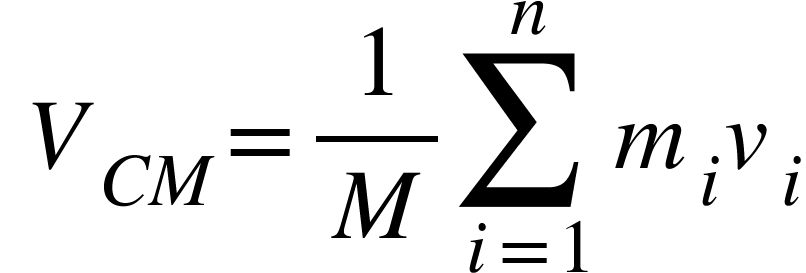$<math xmlns="http://www.w3.org/1998/Math/MathML"><mspace linebreak="newline"/><mo> </mo><msub><mi>V</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>=</mo><mfrac><mn>1</mn><mi>M</mi></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msub><mi>v</mi><mi>i</mi></msub></math>$ ……………….. (1)

Also, $m_{i}v_{i}$= momentum of i’th particle of the system. Then,

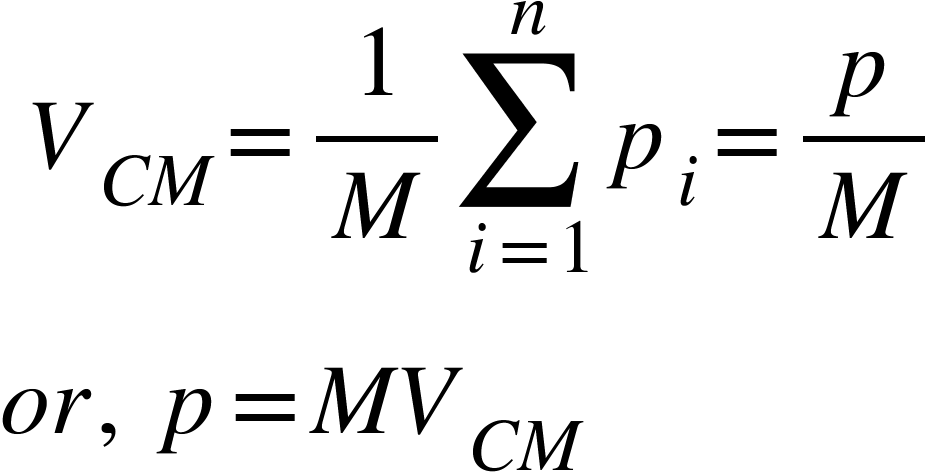
$<math xmlns="http://www.w3.org/1998/Math/MathML"><mspace linebreak="newline"/><mo> </mo><msub><mi>V</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>=</mo><mfrac><mn>1</mn><mi>M</mi></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>p</mi><mi>i</mi></msub><mo>=</mo><mfrac><mi>p</mi><mi>M</mi></mfrac><mspace linebreak="newline"/><mi>o</mi><mi>r</mi><mo>,</mo><mo> </mo><mi>p</mi><mo>=</mo><mi>M</mi><msub><mi>V</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub></math>$

$p$ is the vector sum of linear momentum or the total linear momentum of the system.

Points to remember:

If there is no external force acting on the system, velocity of centre of mass of the system remains constant.
If there is no external force acting on the system, the vector sum of linear momentum remains constant.

Acceleration of center of mass:

Differentiating equation (1), we get,

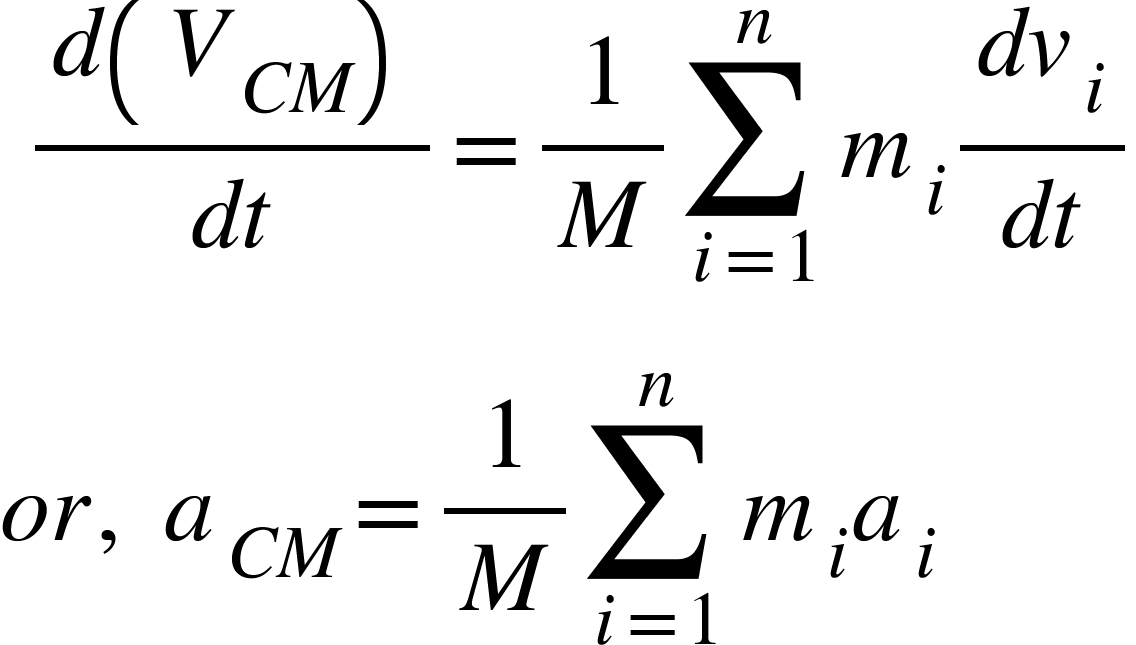
$<math xmlns="http://www.w3.org/1998/Math/MathML"><mspace linebreak="newline"/><mo> </mo><mfrac><mrow><mi>d</mi><mfenced><msub><mi>V</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub></mfenced></mrow><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><mo>=</mo><mfrac><mn>1</mn><mi>M</mi></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><mfrac><mrow><mi>d</mi><msub><mi>v</mi><mi>i</mi></msub></mrow><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><mspace linebreak="newline"/><mi>o</mi><mi>r</mi><mo>,</mo><mo> </mo><msub><mi>a</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>=</mo><mfrac><mn>1</mn><mi>M</mi></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msub><mi>a</mi><mi>i</mi></msub></math>$

Where, $d(v_{i})/dt=a_{i}$= acceleration of i’th particle of the system

If $m_{i}a_{i}=F_{i}$= force acting on i’th particle of the system, then:
$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>a</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>=</mo><mfrac><mn>1</mn><mi>M</mi></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><mfenced open="[" close="]"><mrow><msub><mi>F</mi><mrow><mi>i</mi><mfenced><mrow><mi>e</mi><mi>x</mi><mi>t</mi><mi>e</mi><mi>r</mi><mi>n</mi><mi>a</mi><mi>l</mi></mrow></mfenced></mrow></msub><mo>+</mo><msub><mi>F</mi><mrow><mi>i</mi><mfenced><mrow><mi>i</mi><mi>n</mi><mi>t</mi><mi>e</mi><mi>r</mi><mi>n</mi><mi>a</mi><mi>l</mi></mrow></mfenced></mrow></msub></mrow></mfenced></math>$

Net force acting on the system is,

$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>F</mi><mi>i</mi></msub><mo>=</mo><mfenced open="[" close="]"><mrow><msub><mi>F</mi><mrow><mi>i</mi><mfenced><mrow><mi>e</mi><mi>x</mi><mi>t</mi><mi>e</mi><mi>r</mi><mi>n</mi><mi>a</mi><mi>l</mi></mrow></mfenced></mrow></msub><mo>+</mo><msub><mi>F</mi><mrow><mi>i</mi><mfenced><mrow><mi>i</mi><mi>n</mi><mi>t</mi><mi>e</mi><mi>r</mi><mi>n</mi><mi>a</mi><mi>l</mi></mrow></mfenced></mrow></msub></mrow></mfenced></math>$

Internal force is produced due to the mutual interaction between the particles of the system. Therefore, from Newton’s third law of motion, we can have,

$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>F</mi><mrow><mi>i</mi><mfenced><mrow><mi>i</mi><mi>n</mi><mi>t</mi><mi>e</mi><mi>r</mi><mi>n</mi><mi>a</mi><mi>l</mi></mrow></mfenced></mrow></msub><mo>=</mo><mn>0</mn><mo> </mo><mo> </mo><mfenced><mrow><mi>a</mi><mi>s</mi><mo> </mo><msub><mi>F</mi><mrow><mi>A</mi><mi>B</mi></mrow></msub><mo>=</mo><mo>-</mo><msub><mi>F</mi><mrow><mi>B</mi><mi>A</mi></mrow></msub></mrow></mfenced></math>$

Therefore,

$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>a</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>=</mo><mfrac><mn>1</mn><mi>M</mi></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><mfenced open="[" close="]"><msub><mi>F</mi><mrow><mi>i</mi><mfenced><mrow><mi>e</mi><mi>x</mi><mi>t</mi><mi>e</mi><mi>r</mi><mi>n</mi><mi>a</mi><mi>l</mi></mrow></mfenced></mrow></msub></mfenced><mo>=</mo><mfrac><mi>F</mi><mi>M</mi></mfrac></math>$

Kinetic energy of the system of particles:

Consider there are $n$ number of particles in a system. If the particles are in motion, the motion of the i’th particle of this system would depend on the external force $F_{i} $acting on it.

If the velocity of i’th particle be $v_{i}$ then its kinetic energy is given by,

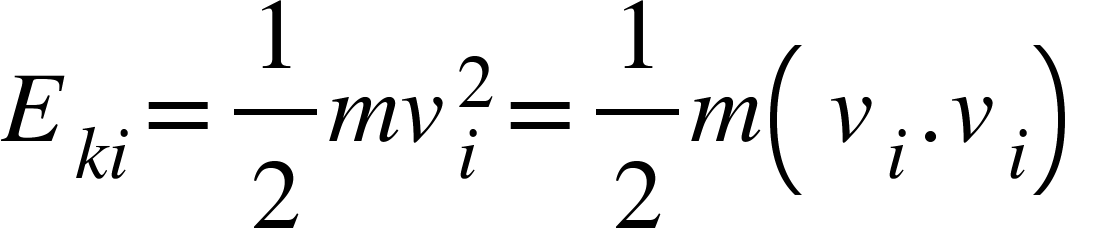$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>E</mi><mrow><mi>k</mi><mi>i</mi></mrow></msub><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>m</mi><msubsup><mi>v</mi><mi>i</mi><mn>2</mn></msubsup><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>m</mi><mfenced><mrow><msub><mi>v</mi><mi>i</mi></msub><mo>.</mo><msub><mi>v</mi><mi>i</mi></msub></mrow></mfenced></math>$ ……………………. (1)

If $r_{i}$ be the position vector of the i’th particle with respect to O and $r_{i}^{‘}$ be the position vector of the center of mass w.r.t. $r_{i}$, then we can write,$r_{i}=r_{i}^{‘}+R_{CM}$ …..(2)
$R_{CM}$ is the position vector of center of mass of the system with respect to O.

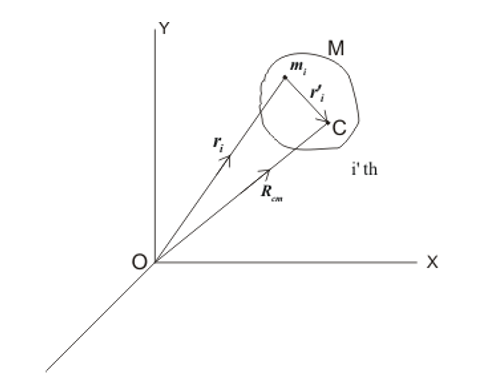
Figure:16.a

Differentiating equation (2), we get

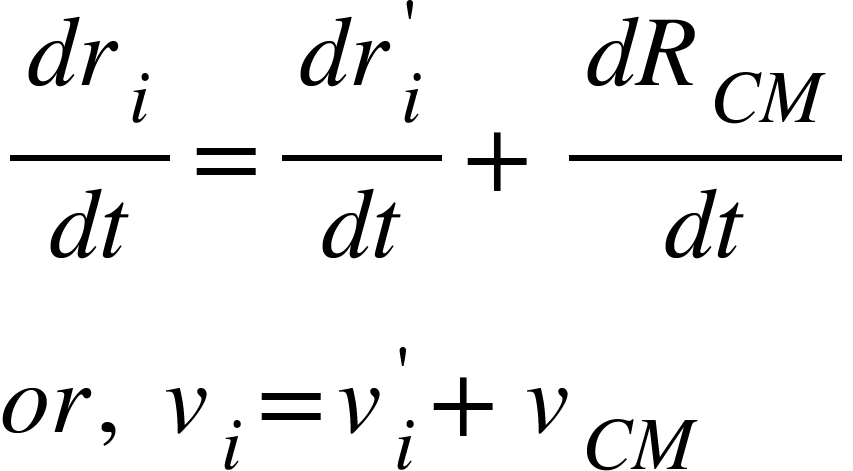$<math xmlns="http://www.w3.org/1998/Math/MathML"><mfrac><mrow><mi>d</mi><msub><mi>r</mi><mi>i</mi></msub></mrow><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><mo>=</mo><mfrac><mstyle displaystyle="true"><mi>d</mi><msubsup><mi>r</mi><mi>i</mi><mo>'</mo></msubsup></mstyle><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><mo>+</mo><mfrac><mstyle displaystyle="true"><mi>d</mi><msub><mi>R</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub></mstyle><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><mspace linebreak="newline"/><mi>o</mi><mi>r</mi><mo>,</mo><mo> </mo><msub><mi>v</mi><mi>i</mi></msub><mo>=</mo><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mo>+</mo><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub></math>$ ………………….. (3)

Putting equation (3) in equation (1), we get,
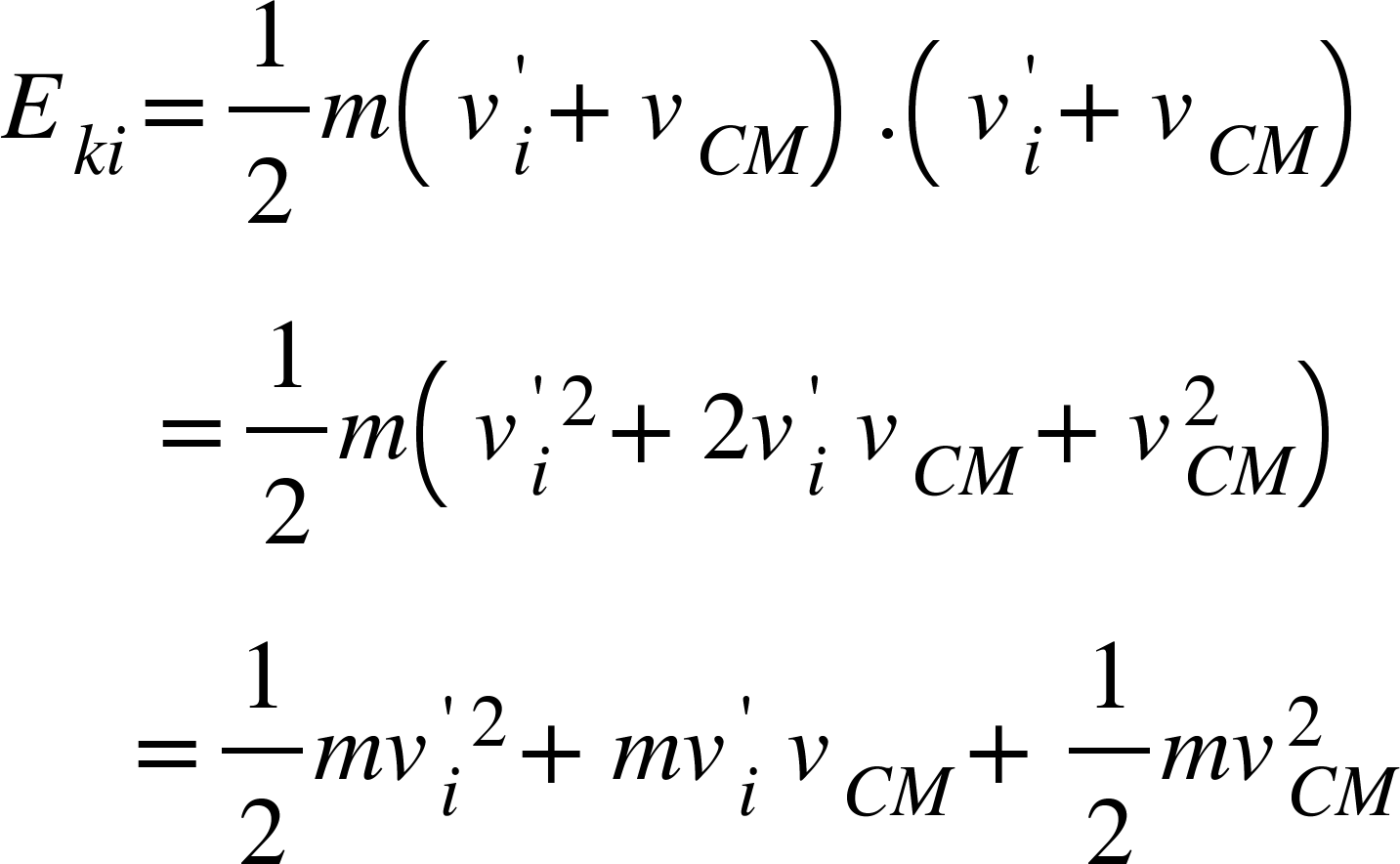
$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>E</mi><mrow><mi>k</mi><mi>i</mi></mrow></msub><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>m</mi><mfenced><mrow><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mo>+</mo><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub></mrow></mfenced><mo>.</mo><mfenced><mrow><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mo>+</mo><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub></mrow></mfenced><mspace linebreak="newline"/><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>m</mi><mfenced><mrow><msup><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mn>2</mn></msup><mo>+</mo><mn>2</mn><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mo> </mo><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>+</mo><msubsup><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow><mn>2</mn></msubsup></mrow></mfenced><mspace linebreak="newline"/><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>m</mi><msup><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mn>2</mn></msup><mo>+</mo><mi>m</mi><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mo> </mo><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>m</mi><msubsup><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow><mn>2</mn></msubsup></math>$

Sum of Kinetic energy of all the particles is given by,

$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>E</mi><mi>K</mi></msub><mo>=</mo><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>E</mi><mrow><mi>k</mi><mi>i</mi></mrow></msub><mo>=</mo><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><mfenced open="[" close="]"><mrow><mfrac><mn>1</mn><mn>2</mn></mfrac><msub><mi>m</mi><mi>i</mi></msub><msup><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mn>2</mn></msup><mo>+</mo><msub><mi>m</mi><mi>i</mi></msub><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mo> </mo><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msub><mi>m</mi><mi>i</mi></msub><msubsup><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow><mn>2</mn></msubsup></mrow></mfenced><mspace linebreak="newline"/><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msubsup><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow><mn>2</mn></msubsup><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msup><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mn>2</mn></msup><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mspace linebreak="newline"/><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msubsup><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow><mn>2</mn></msubsup><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msup><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mn>2</mn></msup><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mfrac><mi>d</mi><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msubsup><mi>r</mi><mi>i</mi><mo>'</mo></msubsup><mspace linebreak="newline"/></math>$

Now from equation (2), we have, $r_{i}^{‘}=r_{i}-R_{CM}$

Therefore, the kinetic energy becomes,

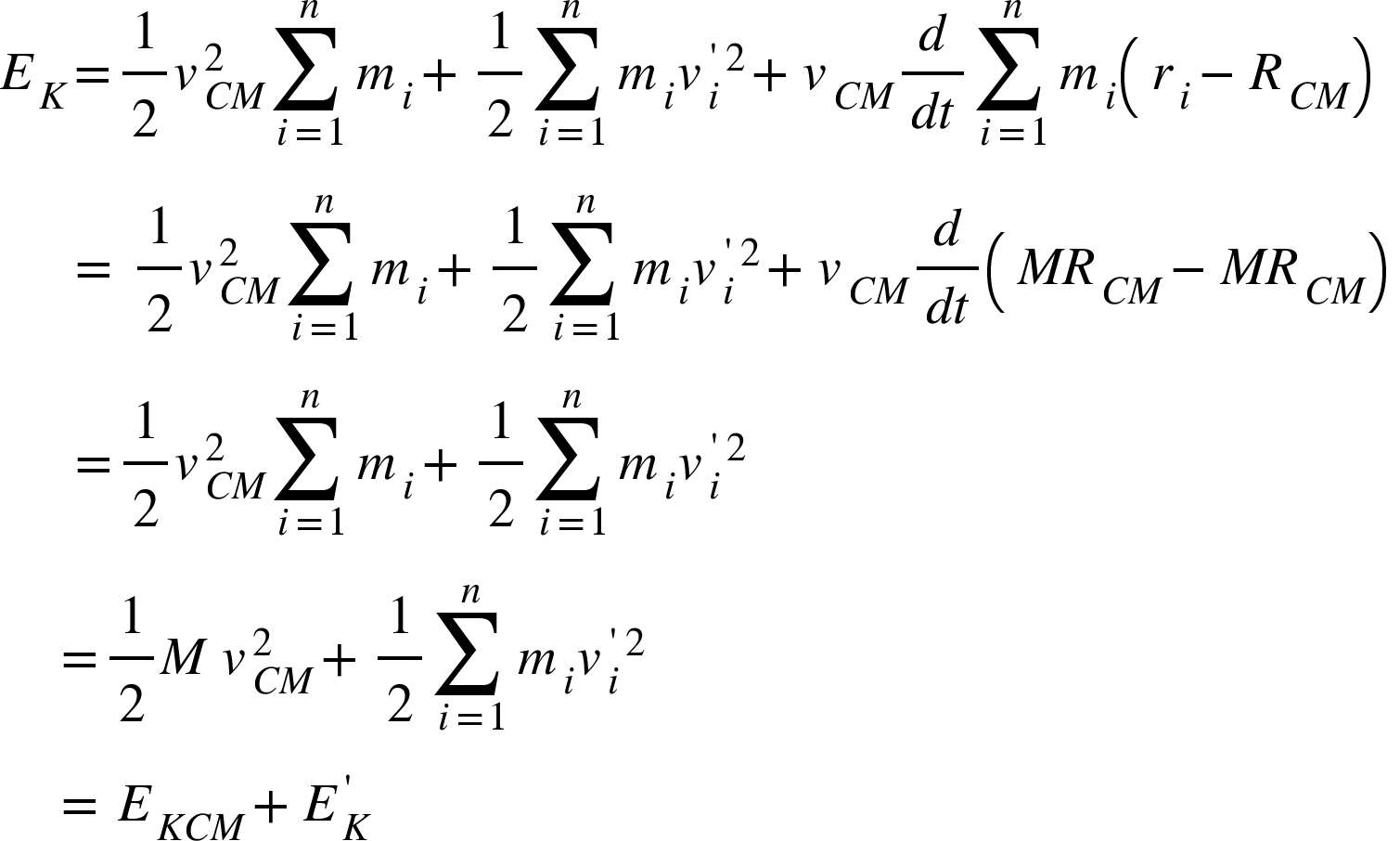
$<math xmlns="http://www.w3.org/1998/Math/MathML"><msub><mi>E</mi><mi>K</mi></msub><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msubsup><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow><mn>2</mn></msubsup><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msup><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mn>2</mn></msup><mo>+</mo><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mfrac><mi>d</mi><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><mfenced><mrow><msub><mi>r</mi><mi>i</mi></msub><mo>-</mo><msub><mi>R</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub></mrow></mfenced><mspace linebreak="newline"/><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo>=</mo><mo> </mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msubsup><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow><mn>2</mn></msubsup><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msup><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mn>2</mn></msup><mo>+</mo><msub><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mfrac><mi>d</mi><mrow><mi>d</mi><mi>t</mi></mrow></mfrac><mfenced><mrow><mi>M</mi><msub><mi>R</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub><mo>-</mo><mi>M</mi><msub><mi>R</mi><mrow><mi>C</mi><mi>M</mi></mrow></msub></mrow></mfenced><mspace linebreak="newline"/><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msubsup><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow><mn>2</mn></msubsup><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msup><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mn>2</mn></msup><mspace linebreak="newline"/><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mi>M</mi><mo> </mo><msubsup><mi>v</mi><mrow><mi>C</mi><mi>M</mi></mrow><mn>2</mn></msubsup><mo>+</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><munderover><mo>∑</mo><mrow><mi>i</mi><mo>=</mo><mn>1</mn></mrow><mi>n</mi></munderover><msub><mi>m</mi><mi>i</mi></msub><msup><msubsup><mi>v</mi><mi>i</mi><mo>'</mo></msubsup><mn>2</mn></msup><mspace linebreak="newline"/><mo> </mo><mo> </mo><mo> </mo><mo> </mo><mo>=</mo><mo> </mo><msub><mi>E</mi><mrow><mi>K</mi><mi>C</mi><mi>M</mi></mrow></msub><mo>+</mo><msubsup><mi>E</mi><mi>K</mi><mo>'</mo></msubsup><mspace linebreak="newline"/></math>$

Where $E_{KCM}$ is the kinetic energy obtained as if all the mass were concentrated at the centre of mass and is the kinetic energy of the system of particles with respect to the centre of mass.