Modes of vibration are particularly, though by no means are exclusively related to musical instruments. It is another shape of vibration, and most of the musical instruments have more than one mode of vibration, because without it, they would be fairly limited in their musical range. Compare the sounds of a violin (with 4 to 7 strings) with a musical triangle, which only emits one note.

When you pluck a stretched string, you always hear a sound with a definite musical pitch. By altering the length, tension or weight of the string, all familiar to musicians, you can alter this pitch. Strings and stretched drumheads are all suitable for producing a variety of vibrations, so they make musical instruments with a wide range of sounds possible. If you used a brick, or a frying pan instead, there is very low scope for musical range, as their vibration modes are very limited.
Types of modes
There are three general types of motions: translations (external), rotations (internal) and vibrations (internal). A diatomic molecule contains only a single motion, while polyatomic molecules exhibit more complex vibrations, known as normal modes.
Harmonics
A harmonic is one of an ascending series of sonic components of those that sound above the audible fundamental frequency. The harmonic spectrum of the sound is made up of the higher frequency harmonics that sound above fundamental. Harmonics can be difficult to perceive distinctly as single components, nevertheless they are there.The simplest description of the vibration of a stretched string shows a pattern in the set of resonance frequencies. Once the lowest (or fundamental) frequency has been fixed by choosing the weight, tension and length of the string, then all the other frequencies are whole-number multiples: if the first is f, then the second is 2f, the third 3f, and the 4th is nf . The frequencies are called the natural frequencies or overtones, and this simple numerical pattern relating them is called a harmonic series: so a stretched string has natural frequencies that are harmonic.
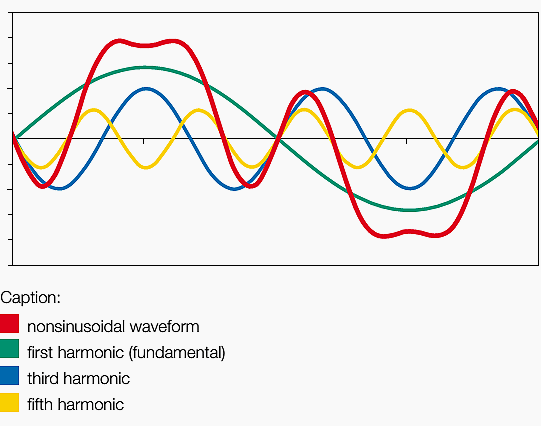
Harmonics have an exceedingly lower volume than the fundamental modes. Harmonics are positive integer multiples of the fundamental. For example, if the fundamental frequency is 50 Hz (which we can also call the first harmonic) then the second harmonic will surely be 100 Hz (50 * 2 = 100 Hz), then the third harmonic is 150 Hz (50 * 3 = 150 Hz).