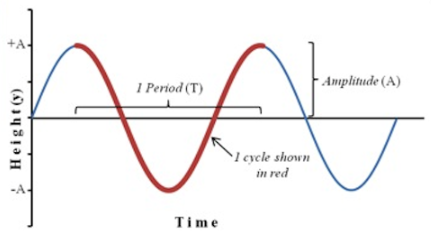
In physics, the phase is the periodic function F, of some of the real variables (t) and phase, is the relative value of that variable in the span of every full period. Typically, it is expressed as an angle. Its expression is on such a scale that it varies by the 1complete full turn as the variable goes through each period. So, if there is an expression of the phase in the degrees then it will be increased by the 360 degrees as there is an increase in the variable by the one period. But if the phase is expressed in the radians, then due to the same increase in the variable the phase will be increased by the 2 pi.
Description
Especially this convention is appropriate for the sinusoidal functions as its value at any argument can be expressed as the sine of the phase multiplied by the factor such as the amplitude of the sinusoid. Instead of the sine, the cosine can also be used depending on the starting of each period. Usually, for the expression of the phase, the whole turn is ignored, as the variable is also the periodic function having the same period as F that causes the repeated scanning of the same range of the angles as the t go through every period.
Numerical Value of Phase Difference
The numerical value of the phase is dependent on the arbitrary point of the starting of each period and on intervals of the angles that each period has to map on. The phase is also used for comparing the periodic function with its shifted version G. If the shift is expressed as a fraction of the period, then by scaling to the angle by spanning the whole turn, one can get the phase offset, phase difference, and phase shift.
Phase Comparison
It is a comparison of the phase of two different waveforms, usually which are having the same nominal frequency. In frequency and time, the main purpose of the phase comparison is the determination of the frequency offset concerning the reference. For the phase comparison, two channeled oscilloscope are used. Two sine signals will be displayed by the oscilloscopes. If the frequencies are the same, then the phase relationship could not be changed and both frequencies will appear as stationary on the oscilloscope. When the frequencies are the same then there is the movement of the test signals, and the references appear as stationery.