Multiplying a vector 
with a positive number n gives a vector 
(= n
) whose magnitude is changed by the factor n, but the direction is same as that 
.
Also, Multiplying a vector 
with a negative number n gives a vector 
(= – n
) whose direction is opposite to the direction of 
and its magnitude is – n times 
.
An example is given:
Diagram (a): Multiplication by a positive number
Diagram (b): Multiplication by a negative number
Figure:6.a
Vector addition and subtraction – graphical method:
Let OA = p be a vector. From the terminal point of p, another vector AB = q is drawn. Then, the vector OB from the initial point of p to the terminal point B of b is called the sum of vectors p and q and is denoted by s = p + q. This is called the triangle law of addition of vectors.
Figure:6.b
From the above diagram, we get,
s = p + q
Or, 
Points to remember:
- Vector addition is commutative i.e. p + q = q + p
- Vector addition is associative i.e. p + q + s = (p + q) + s = p + (q + s) = (p + s) + q
- p + 0 = p
- p + (- p) = 0
Now, the above diagram can be expressed as below:
Figure:6.c
The direction of vector b is reversed and then the vector addition process is followed.
Then, it can be written as,
s = p – q = p + (- q)
Vector addition – analytical method:
Parallelogram law: If two vectors P and Q are represented by two adjacent sides of a parallelogram both pointing outwards, then the diagonal of the parallelogram represents the resultant of P and Q.
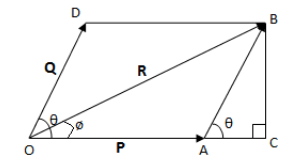
Figure:6.d
From the diagram, we get,
R = P + Q
BC is normal to OC.
From the geometry of the diagram,
$OB^{2}=OC^{2}+CB^{2}$ ……………………….. (1)
Now, AC = $Qcos\theta $
So, OC = P + $Qcos\theta $
And BC = $Qsin\theta $
From equation (1),
$R^{2}=(P + Qcos\theta )^{2}+$$(Qsin\theta )^{2}$
Or, $R=\sqrt{P^{2}+Q^{2}+2PQcos\theta }$……………………….. (2)
The direction of the resultant vector R from vector A is given by,
$\tan \varphi =BC/OC$
Or, $\tan \varphi =\frac{Qsin\theta }{P + Qcos\theta }$
Or, $\varphi =\tan ^{-1}(\frac{Qsin\theta }{P + Qcos\theta })$ ……………….. (3)
Equation (2) and (3) give the magnitude and direction of the resultant vector respectively.
Points to remember:
- As $R=\sqrt{P^{2}+Q^{2}+2PQcos\theta }$, R will be maximum when $\cos \theta $= 1 i.e. $\theta =0$. This signifies that vectors are parallel. So, $R_{\max }=P+Q$.
- R will be minimum when $\cos \theta $= – 1 i.e. $\theta =180$. This signifies that vectors are antiparallel. So, $R_{\min }=P-Q$.
Zero vector:
Zero vector is a vector whose initial and terminal points are same. The magnitude of the zero vector is always zero. This is also called null vector. The zero vector is denoted by 
.
When a zero vector is added or subtracted from a vector, then the result is the vector itself in each case.
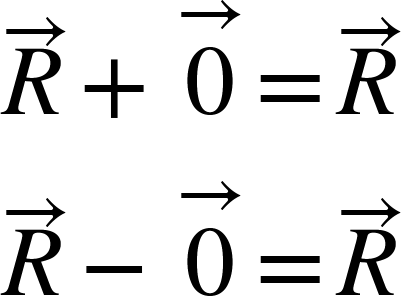
Resolution of vectors:
If any two nonzero vectors 
are in a plane with different directions and 
be another vector in the same plane, then 
can be expressed as a sum of two vectors – one multiplying 
by a real number and the other by another real number.
, where $\alpha $and $\beta $ and are real numbers
So, vector 
has been resolved into two component vectors i.e.
and 
.
Resolution in two dimensions:
Consider a vector 
vector lies in XY plane such that, 
Now, 
, where are unit vectors along the X and Y – axis
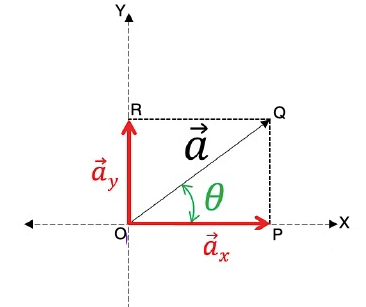
Figure:6.e
So, 
Or, 
The magnitude $\vert a\vert =\sqrt{a_{x}^{2}+a_{y}^{2}}$
And direction, $\theta =tan^{-1}(a_{y}/a_{x})$
Multiplication of vectors:
Dot product:
The scalar product or dot product of any two vectors 
is written as 
.
The dot product is equal to the product of their magnitudes with cosine of angle between them.
Scalar product will be maximum when $\cos \theta $= 1, so, vectors are parallel.
Then, 
Component of 
along c = $b cos\theta $
Or,
= 
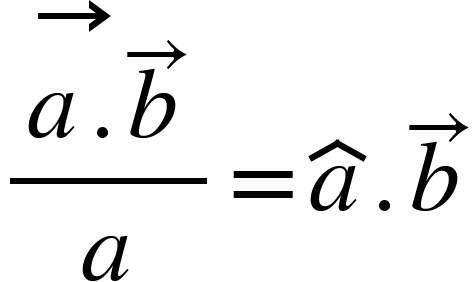
Similarly, the component of 
along 
is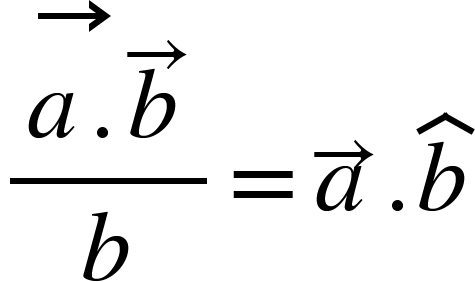 
Cross product:
The vector product or cross product of any two vectors 
is denoted by 
.
It is defined as 
Where $\theta $ is the angle between 
and ${n}$ is the unit whose direction is given by the right-hand thumb rule.
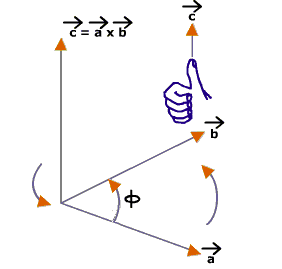
Figure:6.f
Stretch your right palm and pace perpendicular to the plane of 
in such a way that the finger is along the vector 
and towards 
when fingers are closed. The direction of thumb gives the direction of ${n}$.
The vector product of two vectors is always a vector perpendicular to the plane containing the two vectors.
The vector product will be maximum if $\sin \theta $=1 or $\theta =90^{0}.$
