Deviation from ideal behavior
Real gases’ behavior generally has an agreement with the ideal gas equation’s predictions within 5
Johannes van der Waals, the Dutch physicist in 1873 was researching for a method or any idea to link behavior of gases and liquids. So, he came up with the detailing of these deviations and with an equation which has the ability to fir the behavior regarding real gases on a wide range of pressures.
Van der Waals felt that 2 assumptions of the “kinetic molecular theory” were uncertain. The kinetic theory presumes that the particles of gas hold a negligible fraction of the net volume of gas. It even presumes between molecules and gas, the force of attraction is zero.
In the first assumption, the pressure is close enough to 1 atm. But the validity of this first assumption is somehow disturbed or what as there is compression of the gas. Assume for some time that molecules or atoms in the gas were all bunched up in one section of the cylinder as in the diagram given below. At pressure under normal conditions, these particles occupy the volume by a negligible limited fraction of gas’ total volume. But at the same time, this holds false at high pressures.
As a consequence, real gases are not as much compressed as the ideal gas at high pressures. Hence, the volume of real gas is much higher than the expected ideal gas equation at high pressures.
There are dual noteworthy situations in which ideal behavior of gases deviates from the particular model:
- Gas molecules which occupy the volume don’t reach the value zero under high-pressure conditions.
- Intermolecular forces’ contribution becomes important under low-temperature conditions.
Equation of Van der Waals and excluded volume
Real gas particles are, in fact, are occupied by a measurable and finite volume. Under the high-pressure condition, deviation from ideal behavior takes place as the finite volume which the gas molecules are occupied with is important in comparison to container’s total volume.
The “Van der Waals equation” changes the ideal gas law to let it free from error for this exclusion regarding volume, and is represented as follows:
P(V – nb) = nRT
The volume available will now be represented as V – nb
Where,
b = constant that is specific to each gas
In this estimation, the gas molecules are evaluated as hard spheres, having a defined (r) radius which can’t overlap with the neighboring particle’s radius.
The constant b is illustrated as:
b = 4 NA⋅ 4/3π⋅ r³
Where,
NA = Avogadro’s number,
r = radius of the molecule
It’s crucial to note that this above equation is applied to ideal gases too. It can be made easy as in the ideal situation; the value of constant b is very much smaller than V which doesn’t make a determinable and significant difference in calculation.
Intermolecular Forces’ effect
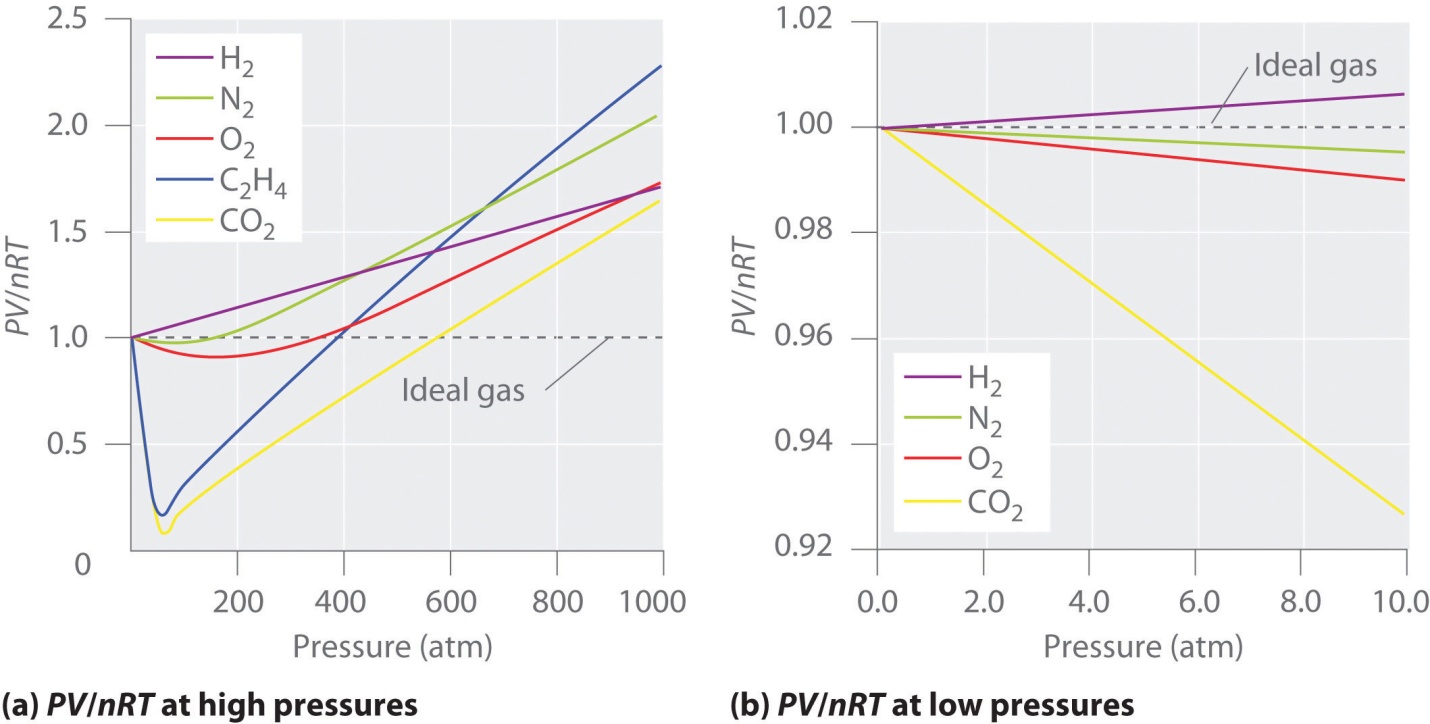
At low temperatures and high pressures, between gas particles, the intermolecular forces can result in causing a noticeable “deviation from the ideal behavior”.