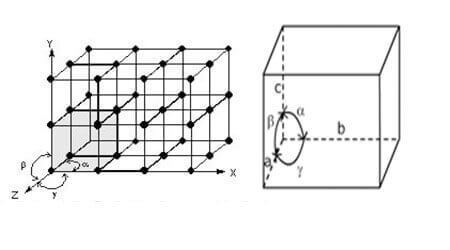
The smallest group of atoms or molecules, whose repetition at regular intervals in three dimensions produces a crystal, is called as a Unit cell. Hence, a unit cell is the smallest portion of a crystal lattice which, when repeated in different directions, generates the entire lattice. Each unit cell is defined in terms of lattice points – the points in space about which the particles are free to vibrate in a crystal.
The position of atoms, molecules, or ions in a solid crystal, relative to one other in space, is usually designated by points. Such a representation is called space lattice. Thus, we define the space lattice as an array of points showing how molecules, atoms or ions are arranged at different sites in three-dimensional spaces.
A unit cell is characterized by:
(i) Its dimensions along the three edges, a, b and c. These edges may or may not be mutually perpendicular.
(ii) Angles between the edges, α (between b and c) β (between a and c) and γ (between a and b). Thus, a unit cell is characterized by six parameters, a, b, c, α, β and γ.
Unit Cell(Cubic)
Types of Unit Cells:
Unit cells can be broadly divided into two categories: i) Primitive and ii) Centred unit cells.
(a) Primitive/ Simple Unit Cells: When constituent particles are present only in the corner positions of a unit cell, it is called a primitive unit cell.
(b) Centered Unit Cells: When a unit cell contains one or more constituent particles present at positions other than corners in addition to those at corners, it is called a centred unit cell.
Centered unit cells are of three types:
(i) Body-Centered Unit Cells (BCC): A unit cell contains one constituent particle (atom, molecule or ion) at its body-centre and eight particles are at its corners.
(ii) Face-Centered Unit Cells (FCC): A unit cell contains one constituent particle present at the centre of each face, along with eight particles at its corners.
(iii) End-Centered Unit Cells (ECC): A unit cell, one constituent particle is present at the centre of any two opposite faces along with eight particles at its corners.
Bravais Lattices: The French crystallographer August Bravais in 1848 showed from the geometrical consideration that there can be only 14 different ways in which similar points can be arranged in a three-dimensional space. Thus, the total number of space lattices belonging to all the seven basic crystal system but together is only 14.
There are seven types of primitive unit cell and they give rise to seven crystal systems.
Seven crystal systems: Cubic, Tetragonal, Orthorhombic, Monoclinic, Hexagonal, Rhombohedral, Triclinic. The seven crystal systems make total fourteen types of unit cells, hence space lattices.
Specifications for the seven basic crystal systems are given in the tabular form:
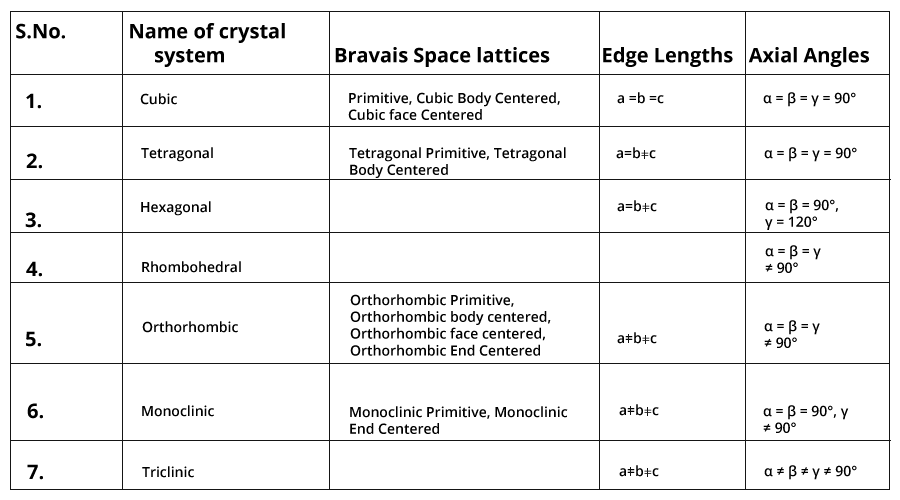
The different types of Bravais lattices are shown below:
The solid states of the majority of metallic elements, some covalent compounds, and many ionic compounds occur as cubic lattices. A key parameter of any lattice is the coordination number; it is defined as the number of nearest neighbors of a particle.
The question arises, how many particles make up a unit cell?
If the particles are of the same size, the higher the coordination number, the greater the number of particles in a given volume. Since one unit cell touches another, with no gaps in a space lattice, so a particle at the corner or face is shared by adjacent unit cells. In cubic unit cells, the particle at each corner is part of 8 adjacent unit cells. So one-eighth of each particle belongs to each unit cell. There are eight corners in a cube, so:
- A simple/ primitive unit cells contain 8 x 1/8 particle = 1 particle.
- A body centered cubic unit cell, contains 8 x 1/8 = 1 particle + 1 particle in the centre, thus, a total of 2 particles.
- A face centered cubic unit cell contains 8 x 1/8 = 1 particle + 1/2 particle in each of the six faces, or 6 x ½ particle = 3 particles, thus a total of 4 particles.