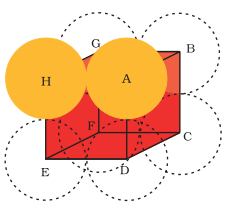
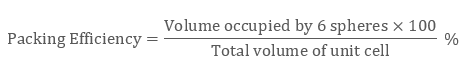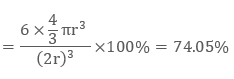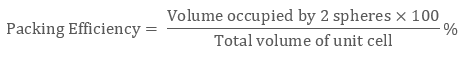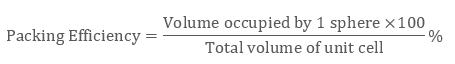As per our knowledge, component particles including ion, molecule, or atom are arranged in unit cells having different patterns. It doesn’t matter in what manner particles are arranged in a lattice, so, there’s always a little space left vacant inside which are also known as “Voids”. Quantitative characteristic of solid state can be achieved with packing efficiency’s help.
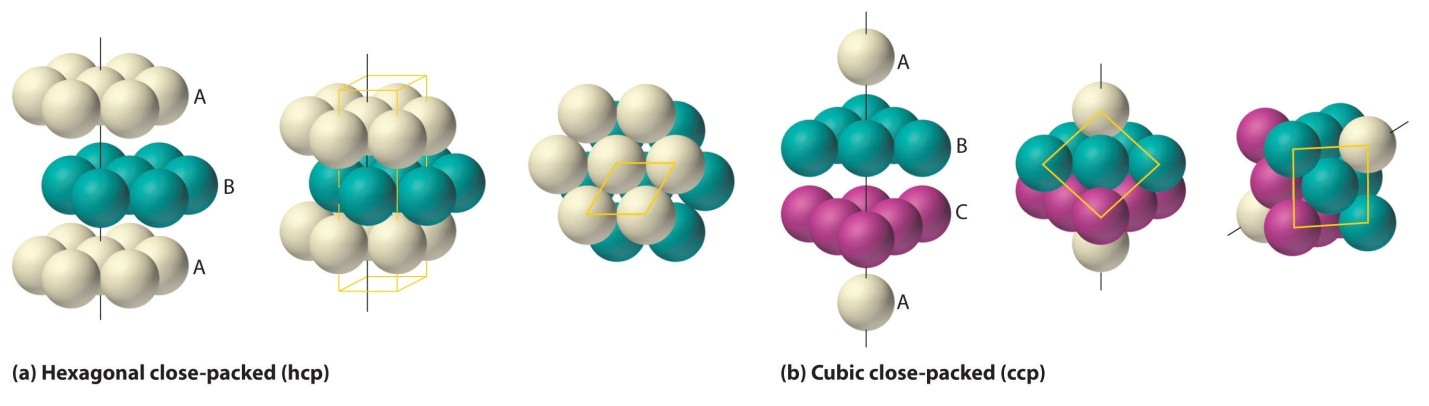
Fig1: Packing efficiency is dependent on atoms’ arrangements and packing type
Packing Efficiency is Mathematically represented as:
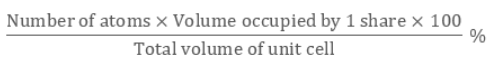
Packing efficiency refers to space’s percentage which is the constituent particles occupies when packed within the lattice. The calculation of packing efficiency can be done using geometry in 3 structures, which are:
- CCP and HCP structures
- Simple Cubic Lattice Structures
- Body-Centred Cubic Structures
Factors Which Affects The Packing Efficiency
Following are the factors which describe the packing efficiency of the unit cell:
- Number of atoms in the structure
- Volume of atoms
- The volume of Unit Cell
HCP and CCP Structures
In both HCP and CCP Structure’s packing, the packing efficiency is just the same. If you want to calculate the packing efficiency in “ccp” structure i.e. cubic closed structure, we should consider the unit cell, having the edge length of “a” and there’s a diagonal face AC in below diagram which is ‘b’.
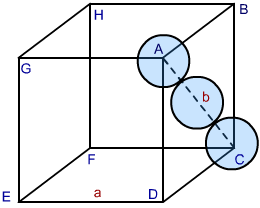
Fig 2: CCP Structure
As per the diagram, the face of the cube is represented by ABCD, then you can see a triangle ABC. Now, take the radius of each sphere to be ‘r’. Having a co-relation with edge and radius of the cube, we take:
In △ ABC, using Pythagoras theorem:
AC2 = BC2 + AB2 ………………Eq 1
∵ BC = AB = a, and AC = b,
So, by substituting the values in Eq. 1
b2 = a2 + a2
b2 = 2a2
b = √2 a….. (2)
Also, edge b of the cube in relation with ‘r’ radius is equal to:
b = 4r … (3)
From (2) and (3):
4r = √2 a
or,
a = 2 √2 r
In ccp structure of the unit cell, as there are four spheres, so the net volume is occupied by them, and which is given by:
4 × 4 / 3 π r3
Further, cube’s total volume is (edge length)3 that is “a3” or if given in the form of radius ‘r’, it is given by (2 √2 r)3, hence, the packing efficiency is given as:
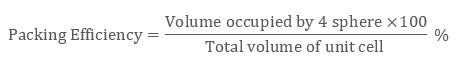
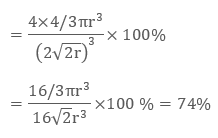
So, the packing efficiency in hcp and fcc structures is equal to 74
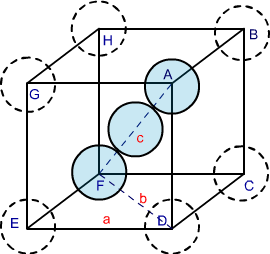
Likewise in the HCP lattice, the relation between edge length of the unit cell “a” and the radius ‘r’ is equal to, r = 2a, and the number of atoms = 6 Examples: Mg, Ti, Be, etc Body-Centred Cubic Structures In the Body-Centered Cubic structures, 3 atoms are arranged diagonally. To determine its packing efficiency, we should be considering a cube having the edge length of “a”, the cube diagonal as “c”, and the face diagonal length as “b”. Fig 3: BCC structure In the △ EFD, as per Pythagoras theorem, b2 = a2 + a2 b2 = 2a2 b = √2 a Further, in △ AFD, as per Pythagoras theorem, c2 = a2 + b2 = a2 + 2a2 c2 = 3a2 c = √3 a Having each sphere with radius, ‘r’: c = 4r √3 a = 4r r = √3/ 4 a As 2 atoms are present in bcc structure, then constituent spheres’ volume will be: 2 × (4/3) π r3 Hence, the packing efficiency of the Body-Centered unit cell or Body-Centred Cubic Structures is 68
Eg.: (Fe) Iron, (Cr), Chromium Simple Cubic Lattice In this lattice, atoms are positioned at cube’s corners only. From the figure below, you’ll see that the particles make contact with edges only. Fig 4: Simple cubic cell So, if the ‘r’ is the radius of each atom and ‘a’ is the edge length of the cube, then the correlation between them is given as: 2a = r ∵ a “simple cubic unit cell” is having 1 atom only, unit cell’s volume is occupied with 1 atom which is: 4 / 3 π r3 And, the volume of the unit cell will be: ( a3) or ( 2a)3 i.e. 8a3 ∴ the packing efficiency of a simple unit cell = 52.4
Eg.: Metals such as Ca (Calcium), and Li (Lithium) Importance of Packing Efficiency