Chemical Thermodynamics: Work
Energy $(\Delta U)$ can cross the boundary of a system in two forms -> Work (W) and Heat (q). Both work and heat refer to processes by which energy is transferred to or from a substance.
$\Delta U=W+q$
Work done by a system is defined as the quantity of energy exchanged between a system and its surroundings. It is governed by external factors such as an external force, pressure or volume or change in temperature etc.
Work (W) in mechanics is displacement (d) against a resisting force (F).
Work has units of energy (Joule, J)
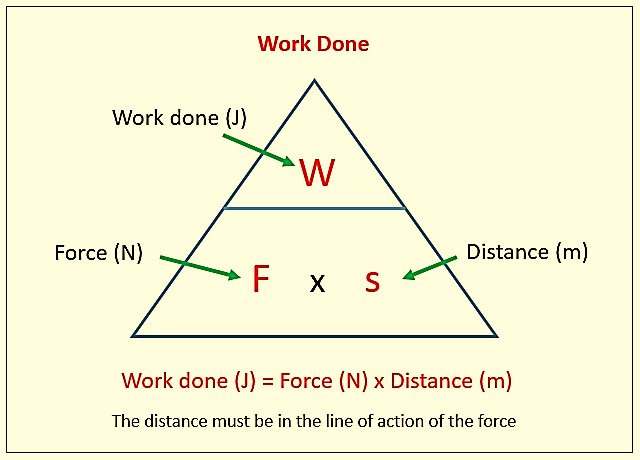
Figure 1: Fundamental formula of work
In thermodynamics, the work is referred by the pressure-volume relationship of a gaseous substance. Energy spent to overcome external force is called work. when is system works against an external pressure or expansion, its internal energy reduces arm the system contracts. When external pressure is applied on a system, the system expands and its internal energy increases.
The work done by a system is calculated by considering the transfer of energy by gas molecules when the piston is moving where the positive direction of x-axis corresponds to expansion.
To calculate how much work a gas has done against a constant external pressure, we use a variation on the previous equation:
$W=-P_{ext}\times \Delta V$
Where, Pext the external pressure (as opposed to the pressure of the gas in the system) and ∆V is the change in the volume of the gas, which can be figured out from the initial and complete volume of the gas:
$\Delta V=V_{2}-V_{1}$
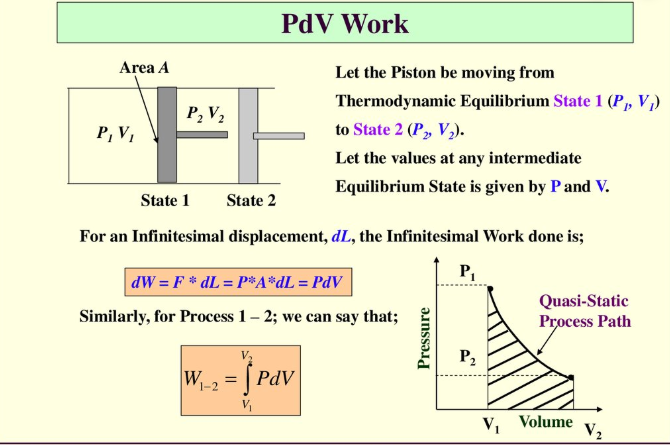
Figure 2: Work done on a piston.
Let the piston move from thermodynamic equilibrium state 1 (P1, V1) to state 2 (P2, V2). Let the values at any intermediate equilibrium state are given by P and V. For infinitesimal displacement, dL, the infinitesimal work done is:
$dW=Fdx=pAdx=pdV$
By integrating both sides, we obtain
$W= \int_{V1}^{V2}{p(V)dV}$
Work done on the system is given by positive sign (+ve) while work done by the system is given a negative sign (-ve). Likewise, work is done on a system, when the volume of a system increases and work is done by a system when its volume decreases. When the gas expands against external pressure, the gas has to transfer some energy to the surroundings. The negative work stops overall energy’s increament of the gas. When the gas is compressed, energy is transferred to the gas so the energy of the gas increases due to positive work.
Since work is energy, it has units of Joules. You may also see other units used, such as atmospheres for pressure and litres for volume, resulting in $L\cdot atm$. We can convert $L\cdot atm$ to to Joules using the conversion factor of $\frac{101.325 J}{1 L\cdot atm}$
Work done by a system is equal to the area enclosed between the P-V curve and the volume axis. It depends on the initial and final stage of the system as well as the path is taken for the process.
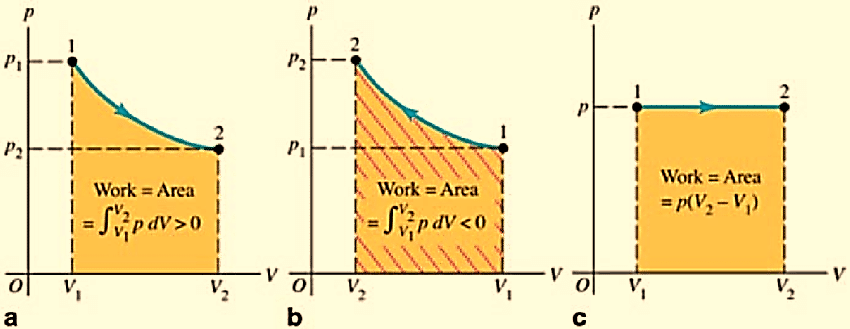
Figure 3a: PV diagram for a system undergoing an expansion with varying pressure
3b: PV diagram for a system undergoing compression with varying pressure
3c: Isobaric process: PV diagram for a system undergoing an expansion with constant pressure.
In quasi-static processes such as isothermal process, each point is in equilibrium and carried out with infinite slowness.
For an isothermal irreversible change, T= constant
$q=-W=p_{external}(V2-V1)$
For an isothermal reversible change, T= constant
$q=-W=nRT\ln \frac{V2}{V1}$
$q=-W=2.303nRT\log \frac{V2}{V1}$
For an adiabatic change,
$q=0$
$\Delta U=W$