Ideal behavior
The Ideal Gas law equation simply demonstrates the relationship between pressure, volume, and temperature for gases. These particular relationships originate from or are derived from Boyle’s Law, Charles’s Law, and Gay-Lussac’s Law.
An ideal gas refers to a theoretical gas, which is composed of several random moving point particles, whose interactions are only based on ideal elastic collisions. The concept of the ideal gas is helpful and beneficial as it obeys the law of ideal gas.
Conditions under which ideal gases displays ideal Behavior?
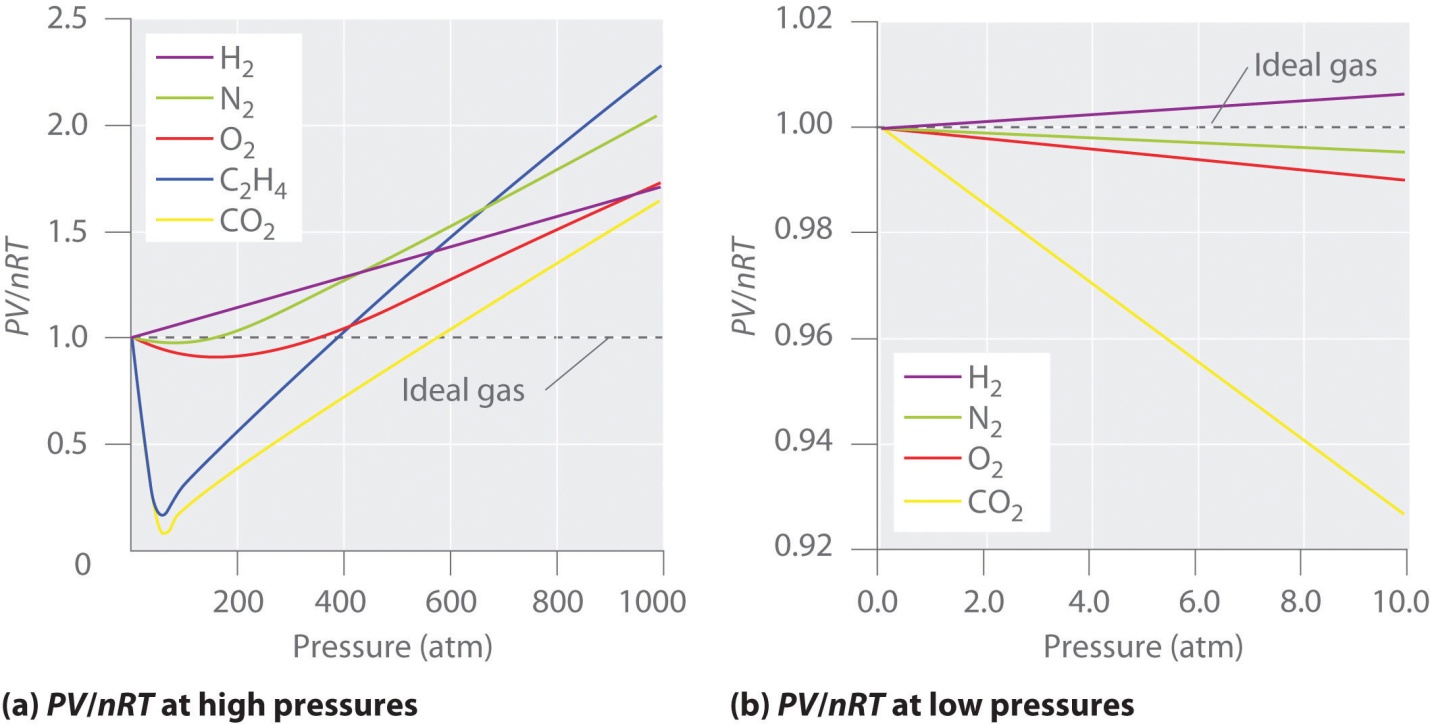
Usually, the behavior of gas is much more similar to an ideal gas at high temperature and low pressure, as potential energy because of the intermolecular forces that become less important in comparison to the kinetic energy of the particles; also, the molecule’s size becomes less important in comparison to the vacant space present between them.
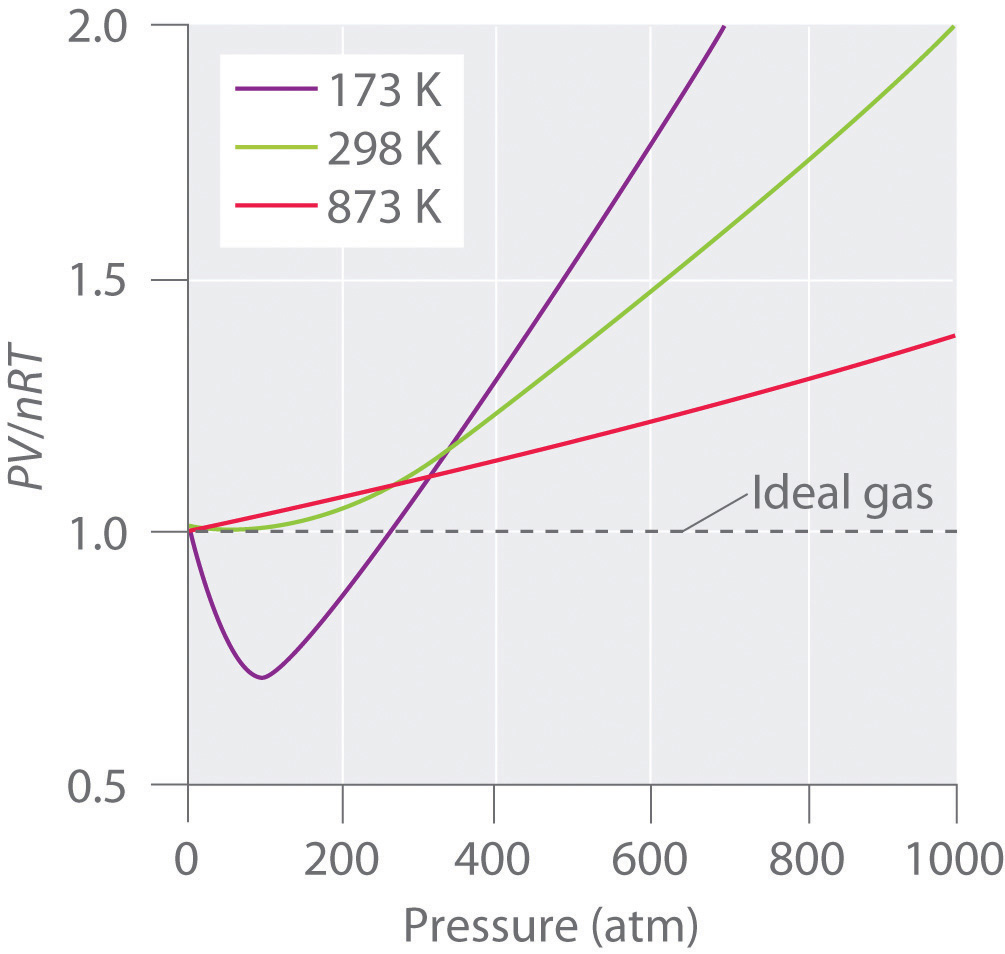
The above graph shows the effect of T on the behavior of real gases.
Ideal gas law is even true for a system which contains many ideal gases; this is referred to as the ideal gas mixture. With many ideal gases in the system, still, these particles are supposed not having any type of intermolecular interaction with one another. The ideal gas mixture divides the total pressure of the system bifurcated into the contribution of the partial pressure of each and every different gas particles.
And in this case, the previous ideal gas equation is re-written as: Pi·V = ni·R·T, where,
Pi = partial pressure of i species
ni = moles of i species
Under low-pressure condition or high temperature conditions, the mixture of gas is believed to be ideal gs mixtures for easy calculation.
When the systems don’t feature high temperature or low pressures, the particles of the gas have the ability to interact with each other; these interactions considerably display ideal gas law’s accuracy.
However, there are other models, like “Van der Waals Equation of State”, that account for intermolecular interaction and for the volume of gas particles.
For an ideal gas, there are 4 commanding assumptions:
- The volume is negligible of gas particles
- The gas particles do not consist of intermolecular forces (whether repulsive or attractive) and they are equally sized with other particles of the gas.
- The particles of the gas randomly move in having an understanding of Newton’s Laws of Motion.
- There’s perfect elastic collision in gas particles with no amount of energy loss.
Actually, there’re no ideal gases. Any particles of gas contain a volume in the system only, which opposes the first assumption given above. In addition, particles of the gas can be of different sizes. For instance, hydrogen gas is noticeably smaller as compared to xenon gas.
Gases within the system have inter-molecular forces with adjacent gas particles, specifically at low temperatures, the spot where particles don’t interact with one another and not move quickly. Though gas particles can randomly move, due to the conservation of momentum and energy within the system as they don’t have the “perfect eleastic collision”.
The ideal gases are rigidly a hypothetical concept, real gases can have the “ideal behavior”, but under specific conditions. Systems containing either high temperatures or very low pressures allow real gases to be supposed as “ideal”.
System’s low pressure enables the particles of the gas to experience fewer inter-molecular forces with other particles of the gas. Likewise, a system containing high temperature enables the gas particles to quickly move inside the system and display lesser inter-molecular forces with one another. Thus, for the purpose of calculation, real gases can thought-out to be “ideal” in either high or low temperature systems.