Chemical Thermodynamics: Standard enthalpy of formation
The standard enthalpy of formation (ΔHf°) for a reaction is the enthalpy change that occurs when 1 mol of a substance is formed from its component elements in their standard states.
When we say “The standard enthalpy of formation of methanol, CH3OH(l) is –238.7 kJ”, it means:
C(graphite) + 2 H2(g) + ½ O2(g) CH3OH(l)
has a value of ΔH of –238.7 kJ.Likewise, for ethanol ∆Hf° [C2H5OH(l)] = – 279 kJ/mol means that when the reaction below is carried out, 279 kJ of energy is released. We may treat ΔHf° values as though they were absolute enthalpies, in order to determine enthalpy changes for reactions. Note that standard enthalpy of formation for an element under standard conditions is 0.Standard conditions refer to a pressure of 1 atm and a specified temperature of 298K (25°C).The standard state of oxygen at 1 atm is O2(g) and for nitrogen, N2(g).The stoichiometry for formation reactions indicates the formation of 1 mole of the respective compound. Hence enthalpies of formation are always denoted with kJ/mol.
The process of calculation of standard enthalpy of formation is as follows:
∆H°rxn = ∑np x ∆Hf°(products) –∑nr x ∆Hf°(reactants)
Where the symbol ‘∑’ signifies the summation of several variables. The symbol ‘n’ signifies the stoichiometric coefficient used in front of a chemical symbol or formula.
In other words
-
- Add all the values for ΔHf° of the products.
- Add all the values for ΔHf° of the reactants.
- Subtract #2 from #1
Example:
Calculate a value for the standard enthalpy of formation of propanone, CH3COCH3(l), where the following are standard enthalpy changes of combustion:
ΔHc/kJmol–1for C(s) = –394kJmol–1, for H2(g)= –286kJmol–1andCH3COCH3(l) = –1821kJmol–1
For the enthalpy change, write an equation representing this change including its state symbols. For the formation of propanone, one mol of the propanone should form the main equation.
3C(s) + 3H2(g) + 0.5O2(g) → CH3COCH3(l)
The reactants in this equation C(s) and H2(g)can be burned to produce CO2(g) and H2O(l).
Other equations related to this reaction are:
3C(s) + 3O2(g) → 3CO2(g) ;nΔH= 3(–394)
where 3 is the stochiometric coefficient of carbon in the main equation.
3H2(g) + 1.5O2(g) → 3H2O(l) ;nΔH= 3(–286)
where 3 is the stochiometric coefficient of H2 in the main equation.
Also, 1 mole of propanone is formed in the main equation so the third equation is be reversed. The sign of ΔH is also changed since the equation is reversed.
3CO2(g) + 3H2O(l) → CH3COCH3(l) + 4O2(g) ;nΔH=+1821
When we add these equations together and cancel down the moles of any substance that appears on both sides of the equation, it results in the main equation and the total of the enthalpy changes gives the enthalpy change for the main equation.
- 3C(s) + 3O2(g) = 3(–394) +
- 3H2(g) + 1.5O2(g)= 3(–286) + Add 1, 2 and 3 3CO2(g) + 3H2O(l) + CH3COCH3(l) + 4O2(g)
- 3CO2(g) + 3H2O(l) = 1821
Cancel the moles of substances which appear on the left side and right side as highlighted above.
This leaves:
3C(s) + 3H2(g) + 0.5O2(g) → CH3COCH3(l)
Where, 3(-394)+3(-286)+1821 = -219 kJ/mol. Therefore, enthalpy of formation of propanone is -219 kJ/mol and this reaction is an exothermic reaction.
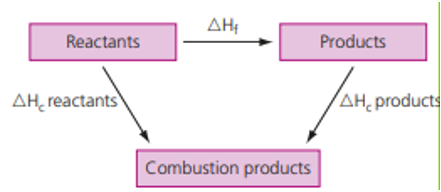
One can also solve the same problem using Hess’s law where,
ΔHf = ΣΔHc (reactants) – ΣΔHc (products)